Основы расчета удароизоляции конструкций приборной аппаратуры. Прибор с амортизаторами. Пример оценки удароизоляции блока

5.6. Основы расчета удароизоляции конструкций

приборной аппаратуры

Для защиты конструкций АПА от ударов используются амортизаторы. Прибор с амортизаторами представляет собой механическую колебательную систему. Удар вызывает сложное движение этой системы, характеристики которого зависят как от параметров системы, так и от параметров удара, в частности от формы ударного импульса (рис. 5.1). Наиболее "жестким" по воздействию на систему является удар в виде прямоугольного импульса. Ударные импульсы с пологими фронтами (синусоидальный, треугольный, трапецеидальный) оказываются более "мягкими". Поэтому прямоугольный и синусоидальный импульсы принято рассматривать как крайние случаи ударных воздействий, для которых производится расчет удароизоляции конструкции.

Модель системы удароизоляции конструкции приведена на рис. 5.2,в, где объект подлежащий удароизоляции представлен массой m , амортизаторы - жесткостью k  [7,21] . Ударный импульс воздействует на платформу, вызывая перемещение системы. В период времени, соответствующий длительности импульса t , движение массы m  носит вынужденный характер. После прекращения действия импульса (t > t) движение массы будет определяться законом свободных колебаний. При этом начальными условиями движения будут смещение и скорость в момент t = t.

В случае воздействия на систему синусоидального ударного импульса и отсутствия в системе неупругих сил, уравнение перемещения массы на отрезке времени  0 < t< t   имеет вид

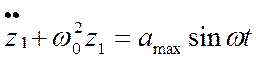 ,                                       (5.12)

где  -  смещение массы т  относительно основания;

 - соответственно смещение объекта (массы) и основания;

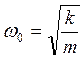 -  частота свободных колебаний системы; k - суммарная жесткость амортизаторов;  - условная частота возбуждения; - максимальная амплитуда ударного импульса.

Для начальных условий  решение (5.12) дает следующее выражение относительного перемещения объекта

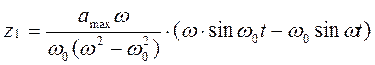.                                  (5.13)

Тогда относительные скорость и ускорение объекта при ударе:

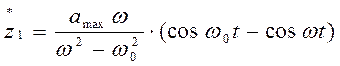  ;                           (5.14)

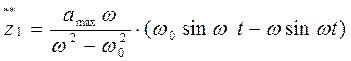.                                       (5.15)

Абсолютное ускорение объекта во время действия удара

.

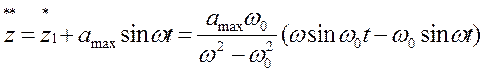Из уравнения движения массы после окончания удара ()    следует решение для относительного перемещения массы:

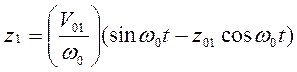,                                              (5.16)

где  и  относительные скорость и перемещение массы в конце ударного импульса   ();  находят из выражений (5.14) и (5.13) при подстановке в них :

 ;       .

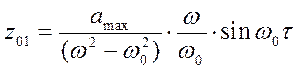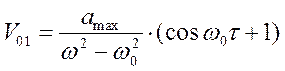После замены в (5.15)  z₀₁ и V₀₁ полученными для них выражениями, решение имеет вид

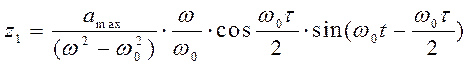             .                   (5.17)

Значение z_1, определяемое согласно (5.17), представляет собой абсолютное перемещение объекта, так как на интервале времени  основание неподвижно, т.е. z_А= 0, z₁ = z.

В результате дифференцирования (5.17) можно найти ускорение объекта

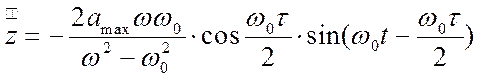  .              (5.18)                                                        

Из анализа (5.17) и (5.18) следует, что движение удароизолируемого объекта отстает от движения основания на угол . Максимальные значения перемещения и ускорения (z_max и  соответственно) достигаются в момент времени 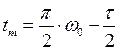(рис. 5.10):

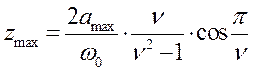 ;                                              (5.19)

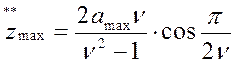 ,                                                (5.20)

где 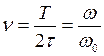   - частотная расстройка; Т -  период свободных колебаний объекта.

Из формулы (5.20) можно получить выражение для определения коэффициента передачи при ударе

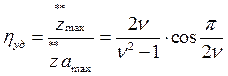    .                                  (5.21)

Зависимость  от частотной расстройки  приведена на рис. 5.11.

Максимальное значение коэффициента передачи соответствует значению  или Т =1,5t. С ростом частотной расстройки значение  плавно уменьшается до нуля.

Аналогичный анализ воздействия прямоугольного ударного импульса позволяет получить следующие выражения для перемещения и ускорения удароизолируемого объекта и коэффициента передачи при ударе:

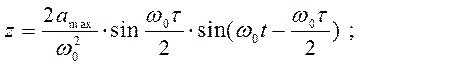                  (5.22)

                  (5.23)

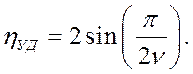                                                            (5.24)

Как следует из (5.24), максимальное значение коэффициент передачи  принимает при частотной расстройке . В интервале значений расстройки  = 0…0,5 наблюдается периодичность значения коэффициента передачи. При значениях >1 коэффициент передачи уменьшается и стремится к нулю