Расчет ударопрочности конструкций приборной аппаратуры. Проверка условия ударопрочности конструкции монтажного основания

связи с тем, что изгибные напряжения в элементах конструкции в конечном счете определяются величиной перемещений (прогибов), расчет ударопрочности конструкции может быть сведен к нахождению запаса прочности элементов при прогибе [7,21,55].

Исходными данными для расчета являются: масса т и геометрические размеры элемента конструкции; характеристики материала (модуль упругости Е ; плотность r   ; коэффициент Пуассона ); перегрузки при ударе  и длительность удара .

Методика расчета заключается в следующем. На первом шаге, по заданным параметрам удара необходимо определить амплитуду ускорения при ударе , значение скорости в начальный момент удара  или эквивалентную высоту падения массы .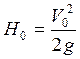

Далее находится частота свободных колебаний конструкции , по значению которой вычисляется максимальный прогиб упругого элемента при ударе. В зависимости от модели, к которой приводится реальная конструкция, расчет частоты свободных колебаний производится по формулам (5.7) - (5.9).

Составляющим максимального прогиба упругого элемента конструкции при ударе является статический прогиб 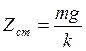. Воспользуемся основной формулой для расчета частоты свободных колебаний, полученной из выражений (5.7)-(5.9):

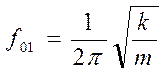                                                   , отсюда   .

Знание статического прогиба , скорости  в начальный момент удара и частоты свободных колебаний позволяет найти максимальный прогиб упругого элемента (максимальное перемещение массы)

                                            

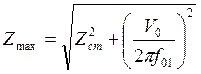
 и полную динамическую деформацию  Z_Д   упругого элемента

                        .

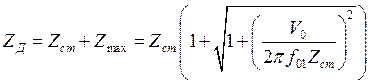Полная динамическая деформация определяет эквивалентную силу удара, приложенную к упругому элементу в точке удара. Допустимое напряжение в элементах конструкции при изгиб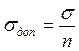е  ,  где - предельное напряжение в материале;  - коэффициент, характеризующий запас прочности:  - коэффициент достоверности определения расчетных нагрузок и напряжений; - коэффициент, характеризующий степень ответственности детали;  -  коэффициент, учитывающий однородность механических свойств материалов.

Изгибное напряжение, возникающее в элементах конструкции при ударе, можно найти через изгибающий момент  и момент сопротивления изгибу  по формуле 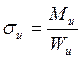. При расчете изгибающего момента исходят из того, что сила  приложена в геометрическом центре упругого элемента. Тогда реакция опор упругого элемента составит 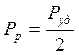, а изгибающий момент 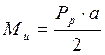, где - геометрический размер элемента конструкции в плоскости изгиба.

Момент сопротивления упругого элемента изгибу 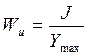, где J - момент инерции сечения элемента относительно оси изгиба ;  - значение координаты от нейтральной оси сечения до поверхности упругого элемента; h - толщина упругого элемента.

Пример проверки условия ударопрочности конструкции монтажного основания

Прямоугольное основание из сплава Д16Т, покрытое диэлектрическим слоем   (поликор) и закрепленное в четырех точках по углам, подвергается удару длительностью  при максимальной перегрузке . Проверить условия ударопрочности конструкции, если размеры основания , толщина пластины , толщина диэлектрического покрытия м.

При решении задачи примем следующие допущения: жесткость конструкции определяется жесткостью монтажного основания; расчетной моделью конструкции является прямоугольная пластина со свободным опиранием всех сторон (см.рис.5.3,б), нагруженная равномерно распределенной массой диэлектрического слоя; прогиб диэлектрического слоя при ударе равен прогибу основания. Решение задачи состоит в определении напряжений, возникающих в основании и диэлектрическом слое при прогибе под действием удара.

Амплитуда ускорения при ударе

.

Начальная скорость в момент удара

.

Для расчета частоты свободных колебаний пластины воспользуемся формулой (5.9). При свободном опирании пластины по контуру и отношении сторон  частотная постоянная . Масса пластины ; масса диэлектрического слоя . Поправочные коэффициенты на материал пластины , на нагружение пластины . Частота свободных колебаний основания

.

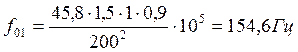Жесткость пластины

.

Статический прогиб пластины

.

Максимальный прогиб упругого элемента

.

Полная динамическая деформация

м.

Эквивалентная сила удара

.

Принимаем минимальное значение коэффициента запаса

, тогда допустимое напряжение в материале основания

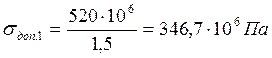, в материале диэлектрического слоя

.

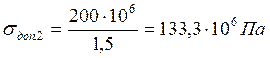Изгибающий момент, действующий на основание и диэлектрический слой

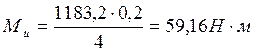, момент инерции сечения основания

.

момент инерции сечения диэлектрического слоя

.

Момент сопротивления изгибу основания

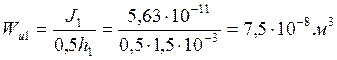, диэлектрического слоя

.

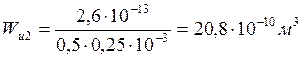Напряжение в материале основания

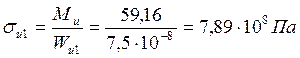, в материале диэлектрического слоя

.

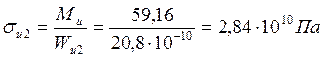Полученные значения напряжений в материале основания и диэлектрического покрытия превышают допустимые величины. Следовательно, необходимые меры по повышению ударопрочности конструкции – увеличение толщины основания и выполнение диэлектрического покрытия не в виде сплошного слоя, а в виде фрагментов с определенными размерами сторон.

Лабораторная работа № 7 К.

 Проверка условия ударопрочности конструкции

монтажного основания

1. Цель работы:

Провести исследование условий обеспечения ударопрочности конструкции прибора и используя программу провести расчет показателей ударопрочности конструкции монтажного основания.

2. Постановка задачи.

На основе анализа параметров конструкции монтажного основания узла в программу необходимо ввести начальные значения по условию задачи. К  вводимым параметрам относятся:

-  длительность удара;

-  максимальная перегрузка;

-  длительность удара;

-  размеры основания;

-  толщина пластины;

-  толщина диэлектрического покрытия;

-  коэффициенты при q.

По данным параметрам программа должна произвести проверку условия ударопрочности конструкции монтажного основания. Для этого вычисляются и выводятся на экран следующие величины:

-  амплитуда ускорения при ударе;

-  начальная скорость в момент удара;

-  масса пластины;

-  масса диэлектрического слоя;

-  частота свободных колебаний основания;

-  жесткость пластины;

-  статический прогиб пластины;

-  максимальный прогиб упругого элемента;

-  полная динамическая деформация;

-  эквивалентная сила удара;

-  допустимое напряжение в материале основания;

-  допустимое напряжение в материале диэлектрического слоя;

-  изгибающий момент;

-  момент инерции сечения основания;

-  момент инерции сечения диэлектрического слоя;

-  момент сопротивления изгибу основания;

-  момент сопротивления изгибу диэлектрического слоя;

-  напряжение в материале основания;

-  напряжение в материале диэлектрического слоя.

3. Описание алгоритма и программы

Программа разработана в объектно-ориентированной среде Delphi