Вычислительные алгоритмы в системе аналитических вычислений Maple. Графики частичных сумм ряда при разных длинах мантиссы, страница 2

Рис. 2. Расчетная схема балки на упругом основании

Завершает постановку задачи задание граничных условий на концах балки — по два на каждом ее конце. Например, в случае свободных концов следует положить равными нулю момент и перерезывающую силу в сечениях  и , а если какой-либо конец жестко защемлен, то полагаются нулю прогиб и угол поворота.

Предположим, что все коэффициенты в системе (3) могут быть представлены сходящимися рядами Маклорена на всей длине балки

.                               (4)

Здесь  являются числовыми матрицами размерности , а  числовыми векторами размерности , компоненты которых определяются из вида соответствующих компонентов матрицы  и вектора .

Решение системы дифференциальных уравнений (3) также ищем в виде ряда Маклорена

                                                     (5)

с неизвестными коэффициентами  — числовыми векторами размерности , которые следует определить из условия удовлетворения дифференциальному уравнению задачи и заданным граничным условиям.

После подстановки в систему дифференциальных уравнений (3) разложения в степенные ряды вектора решения (5) и коэффициентов системы в виде (4) и приравнивания коэффициентов при одинаковых степенях независимой переменной  получим систему линейных уравнений относительно неизвестных коэффициентов в разложении решения

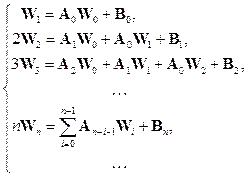
Неизвестные векторы , , этой бесконечной системы можно представить через вектор начальных параметров  путем последовательных подстановок в правые части уравнений выражений для входящих в них векторов  через вектор начальных параметров:

,

,

.  .  .

Теперь решение (5) системы дифференциальных уравнений изгиба балки (3) может быть записано в виде

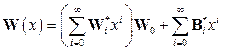,                                        (6)

где матрицы  размерности  и векторы  размерности  представляются выражениями, в которые входят известные матрицы  и векторы  из (4).

      

а                                                                  б

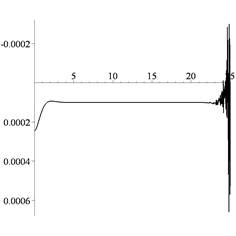
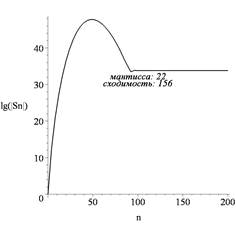
Рис. 3. Прогиб  балки (а) и частичные суммы (б) ряда (10) при проявлении вычислительной неустойчивости

Завершает решение задачи определение четырех компонентов вектора  из системы четырех линейных уравнений, получающейся из условия удовлетворения полученного решения граничным условиям задачи (по два на каждом конце балки).

Для исследования вычислительной устойчивости алгоритма метода начальных параметров рассматривалась бетонная () балка длиной , шириной , высотой , лежащая на упругом основании Винклера с постоянным коэффициентом постели . На левом конце балки действует нормальная к ее продольной оси сила , угол поворота сечения равен нулю . Правый конец балки свободен от нагрузок , . Для исключения отрыва точек подошвы балки от основания, к ней дополнительно приложена равномерно распределенная по всей длине нагрузка интенсивности .

Исследовалось влияние длины мантиссы на достоверное суммирования рядов решения (6) на правом конце балки () на примере ряда

                                                         (7)

в представлении прогиба балки

.

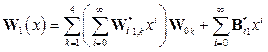Природа вычислительной неустойчивости алгоритма метода начальных параметров аналогична природе вычислительной неустойчивости алгоритма суммирования степенного ряда для синуса: возрастание значений частичных сумм до очень большого значения с последующим их убыванием до истинной величины.

      

а                                                                     б

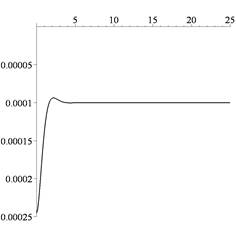
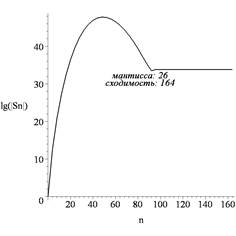
Рис. 4. Прогиб  балки (а) и частичные суммы (б) ряда (7) без проявления вычислительной неустойчивости

На рис. 3,а представлена кривая прогиба  балки при расчетах с 22 цифрами в мантиссе. Ряд (7) для этого случая вычислен с максимально возможной точностью (добавление членов ряда с номерами, большими 156, уже не изменяет полученную сумму ряда). На рис. 3,б показан график его частичных сумм в полулогарифмической шкале и отображен номер члена ряда, добавление которого к вычисленной сумме не изменяет ее значения. Хотя сумма ряда и вычислена с предельно возможной для данного случая точностью, однако она далека от истинного значения, а это и приводит к недостоверным вычислениям на правом конце балки, что и наблюдается на рис. 3,а. Вычисленная сумма ряда , тогда как точное значение (вычисленное с мантиссой длиной 100) равняется . Погрешность составляет величину порядка .

Увеличение длины мантиссы до 26 цифр приводит к достоверным результатам, что можно видеть из графиков рис. 4. В этом случае для вычисления суммы ряда необходимо учесть 164 члена ряда и ее значение равняется .

Заключение

В работе показаны возможности использования аналитических систем в процессе обучения студентов вычислительной математики, а также их преимуществ для реализации вычислительно-неустойчивых алгоритмов. Возможность выполнения расчетов с мантиссой практически неограниченной длины (в Maple максимальное значение длины мантиссы можно устанавливать равным 268435448) по существу снимает проблему вычислительной неустойчивости численных и численно-аналитических алгоритмов. Однако за такое удобство приходится платить скоростью выполнения программ (системы аналитических вычислений интерпретируемы), а для ее увеличения необходимостью наличия на компьютере оперативной памяти большого объема (для некоторых задач до 4Гб).

Литература

1. Матросов А. В. Maple 6. Решение задач высшей математики и механики. СПб.: БХВ-Петербург, 2001. — 528 с.

2. Матросов А. В. Численно-аналитический алгоритм метода начальных параметров. // Вестник СПбГУ, Сер. 10, 2009, вып. 2. С. 72-81.