1 бар соответствует давлению 750 мм. рт. ст. или соответствует высоте водяного столба – 10,4 м.
Измеряют манометрами.
Удельный объем
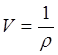
Состояние идеального газа может определятся значениями любых двух параметров.
Идеальный газ – модель газа, где молекулы газа не имеют объема.
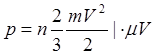
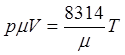
Уравнение состояния реального газа
или уравнение Ван-Дер-Ваальса
Учитывает собственный объем молекул силы сцепления между молекулами.
-учитывает силу сцепления между молекулами
b – учитывает собственный объем молекулы.
Водяной пар не поддается уравнению Ван-дер-Ваальса.
В водяном паре присутствуют одиночные, двойные, … , пятирные молекулы.
Они носят не устойчивый характер. Происходит постоянный распад этих молекул и образование вновь (ассоулация и диссоулация).
Уравнение для водяного пара составлено выдающимися советскими учеными Вукаловичем и Новиковым И.И.
Оно учитывает ассоциацию и диссоциацию молекул. Имеет сложный вид и писать мы его не будем. На основании этого уравнения составляются таблицы и диаграммы водяного пара
1.2. Первый закон термодинамики
Теплоемкость – это количество теплоты которое необходимо для того чтобы нагреть 1кг вещества на1 С.
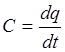
Нас обычно интересует среднее значение
теплоемкости в зданном интервале температур. 
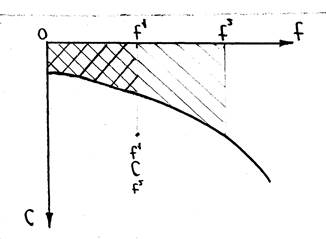
Теплоемкость бывает массовой, объемной, мольной (1кг, 1 м, 1 моль).
Теплоемкость рабочего тела зависит от вида процесса.
а). Изохорический процесс. V = const ;
A = 0 ; dU = m/m cvm (T2 - T1) ; (1.2)
Q = dU ; Q = m/m cvm (T2 - T1) , (1.3)
где m - масса газа ; m - масса одного киломоля газа ; cvm - теплоемкость одного киломоля газа при постоянном обьеме ; T1 , T2 - начальный и конечный температуры газа .
б). Изобарный процесс. Р = const ;
A = PdV или A = m/m Rm (T2 - T1) ; dU = m/m cvm (T2 - T1) ; (1.4)
Q = U + A , Q = m/m Rm (T2 - T1) + m/m cvm (T2 - T1) = m/m cpm (T2 - T1) , (1.5)
где cpm - теплоемкость одного киломоля газа при постоянном давлении;
Rm = 8,31 Дж/(моль К) - универсальная газовая постоянная.
в). Изотермический процесс. T = const ;
A = m/m Rm TlnV2/V1 ; dU = 0 ; (1.6)
Q = A ; Q = m/m Rm TlnV2/V1, (1.7)
где V1, V2 - начальный и конечный обьемы газа.
г). Адиабатный процесс. Q = 0 ;
А = -dU = m/m cvm (T2 - T1) / (g - 1) ; (1.8)
A = m/m Rm T1 [1 - (V1/V2)g -1] / (g - 1) ; (1.9)
A = m/m Rm T1 [1 - (P2/P1) (g -1) / g ] / (g - 1) . (1.10)
где g = cp / cv - показатель адиабаты.
Политропный процесс- такой процесс в котором теплоемкость может иметь любые, но постоянные для данного процесса значения. (“-“).
Работа
Рассмотрим только рвновесный процессв термодинамике.
Условия равновесного процесса:
1.Бесконечные медленные перемещения поршня (время перемещения поршня на заметную величину должно быть больше времени ---- молекул);
2.Разница температур между источником теплоты и рабочим телом ----;
3.Отсутствует внешний необратимый теплообмен с окружающей средой;
4.Отсутствуют внешнее и внутреннеее трение. Внешнее – между поршнем и стенками, внутреннее между --- и молекулами.
5.Отсутствует химическая реакция.
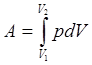
Работа как и теплота являются функцией процесса.
Внутренняя энергия
Для определения значения внутренней энергии рассмотрим процесс V=const
Формулировка: Теплота подведенная к термодинамической системе расходуется на изменение внутренней энергии и на совершение работы.
Теплота которая подводится знак “+”, выводится – “-“
1.3. Второй закон термодинамики
В этом процессе 
и вся теплота, подведенная к системе
расходуется на изменение внутренней энергии.
Поскольку внутренняя энергия является функцией состояния, то этой формулой можно пользоваться в любом процессе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.