Выработка решений в условиях определенности. Постановка задачи принятия решения по скалярному показателю

методы, основанные на динамическом программировании Беллмана;

методы, использующие принцип максимума Понтрягина.

В основу прямых методов положена аппроксимация исходной задачи с непрерывным временем задачей с дискретным временем. При этом временной интервал [Тн, Тк] обычноквантуется с постоянным шагом, дифференциалы в уравнениях движения заменяются отношениями конечных разностей, а интегралы (если они содержатся в постановке задачи) - конечными суммами. В результате получается задача математического программирования с новыми переменными x(k),a(k), гдеk= 0, 1, ..., К, причем К = (Тк - Тн - Δt)/ Δt, где Δt - шагквантования.

Динамическое программирование было создано на рубеже 50-х гг. XX столетия группой американских специалистов, однако, благодаря ряду идей и практических приемов, предложенных Р. Беллманом, оно часто связывается с его именем. Динамическое программирование применяется как метод решения задач оптимального управления непрерывного и дискретного типов с целевой функцией достаточно произвольного вида.

Постановка задачи принятия решений по векторному критерию

Cложность проблемы принятия решений по векторному критерию даже в условиях определенности связана не столько с вычислительными трудностями, сколько с концептуальной обоснованностью выбора оптимального решения. Невозможно строго математически доказать, что выбранное решение наилучшее, - любое решение из числа недоминируемых, то есть неулучшаемых одновременно по всем частным критериям, может оказаться наилучшим для конкретного ЛПР в конкретных условиях. С этой же точки зрения не имеет смысла говорить о наилучшем решении вообще. Это может считаться основной аксиомой обоснования решений по нескольким критериям.

Постановказадачи. Сравнение альтернатив по векторному критерию прежде всего будем осуществлять по следующему очевидному правилу: всякая альтернатива не хуже любой другой, если для нее значение векторного критерия не менее предпочтительнее значения критерия другой альтернативы, то есть

где a₁,  a₂- альтернативы;

W(a) - векторный критерий.

Будем разделять методы построения функции выбора по степени обоснованности и в связи с этим введем два класса методов: аксиоматические и эвристические.

Как можно предположить из названий, аксиоматические методы основаны на предварительном выдвижении и проверке справедливости некоторых аксиом и используют преимущественно количественную информацию о предпочтениях.

В аксиоматических методах установление вида и параметров функции ценности осуществляется на основе анализа комплексной количественной информации о решаемой задаче и предпочтениях ЛПР. Разумеется, получение подобной информации и ее обработка требуют существенных материальных и временных затрат, привлечения аналитиков высокой квалификации и общей высокой теоретической подготовки ЛПР. Все это ограничивает широкое распространение аксиоматических методов на практике.

Эвристические методы, наоборот, очень просты как по идее, так и по форме реализации. Все они в той или иной мере основаны на сведении исходной задачи с векторным критерием к задаче (совокупности задач) со скалярным критерием. Полученное путем оптимизации каждой такой задачи решение затем обязательно должно анализироваться ЛПР и при необходимости корректироваться в направлении придания более предпочтительных значений тем или иным частным критериям. Такая процедура повторяется до тех пор, пока не будет получено приемлемое, с точки зрения ЛПР, решение.

Рассмотрим наиболее употребительные из способов построения функции выбора в порядке последовательного усложнения информации о предпочтениях ЛПР. Как уже отмечалось, самая простая и, следовательно, надежная информация - информация о независимости частных критериев по предпочтению. Построенная на ее основе функция выбора позволяет выделять так называемые эффективные стратегии (недоминируемые альтернативы).

Пусть известно, что предпочтения ЛПР на множестве векторных оценок не изменяются скачком и для любой точки хможно так изменять ее компоненты х_i, что исходная и новая точки будут одинаковы по предпочтительности в смысле достижения цели операции. Формально справедливость такого допущения означает, что имеется некоторое подмножество точек, которым можно поставить в соответствие (приписать) некоторую определенную ценность, которую можно измерять с помощью функции V(x).

Обратимся к рис. 5.1, на котором представлены графики двумерных кривых равноценности (линии одинаковой предпочтительности) V(x) = const.

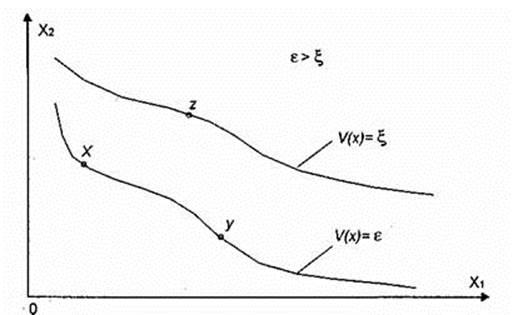
Рис. 5.1. Графики двумерных кривых равноценности

Если векторные оценки хи у одинаковы по предпочтительности (рис. 5.1), то они лежат на одной кривой равноценности V(x) = ε, если точка