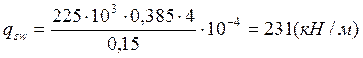Конструктивная схема монолитного ребристого перекрытия, назначение размеров элементов перекрытия. Компоновка конструктивной схемы резервуара, страница 6

;

;

с₀ определяем по формуле 3.2.10:

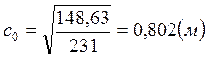, так как с₀ лежит в пределах , то трещины развиваются в приопорной зоне, расчёт продолжаем с полученным с₀.

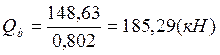, так как – то требуется установка поперечной арматуры.

;

 – условие 3.2.3 выполнено, прочность обеспечена. Принимаем поперечную арматуру  Æ7А–IV, с шагом 150(мм).

2) Второй пролёт:

Назначаем диаметр поперечной арматуры из условия свариваемости:

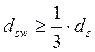,                                                                                                       (3.2.12)

где d_s=18(мм)  – диаметр продольной арматуры в первом пролёте.

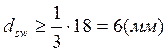, принимаем d_sw=7(мм), A_sw=0,385(см²), S₁=150(мм), n=2.

Далее определяем q_sw и M_b соответственно по формулам 3.2.7 и 3.2.5:

 

;

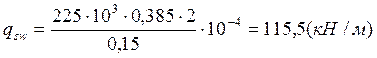
с₀ определяем по формуле 3.2.10:

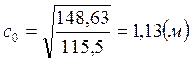, так как с₀ лежит в пределах , то трещины развиваются в приопорной зоне, расчёт продолжаем с полученным с₀.

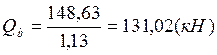, так как – то требуется установка поперечной арматуры.

;

 – условие 3.2.3 выполнено, прочность обеспечена. Принимаем поперечную арматуру  Æ7А–IV, с шагом 150(мм).

3.3 Построение эпюры материалов, обрыв арматуры

При определении места обрыва продольной арматуры необходимо учитывать, что в каждом каркасе один стержень выводится на опоры. Если рабочих стержней в арматуре больше одного, остальные стержни можно оборвать в соответствии с эпюрой изгибающих моментов в балке. При этом учитывается несущая способность сечения:

,                                                                                      (3.3.1)

где  и  – для сечения с рабочей арматурой, расположенной в ребре (полка сжата);

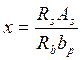 и  – для сечения с рабочей арматурой, расположенной в полке (полка растянута);

 - оставшаяся после обрыва стержней площадь арматуры.

На эпюре моментов находится место теоретического обрыва продольной арматуры. В этом месте величина изгибающего момента в сечении от расчетных нагрузок должна быть равна выше моменту сечения, армированного оставшейся после обрыва арматурой. В сечении у места обрыва определяется поперечная сила и вычисляется величина заделки арматуры за место ее теоретического обрыва :

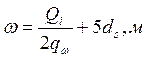,                                                                                                (3.3.2)

где,  – диаметр обрываемой продольной арматуры, мм;

 – значение поперечной силы в точке обрыва, кН;

– усилие, воспринимаемое поперечной арматурой, отнесенное к единице длины изгибаемого элемента, в сечении у места теоретического обрыва, кН/м.

 если это условие не выполняется то, принимаем .

1) для крайнего пролета:

Подсчитаем величину момента для 3Æ20A – IV:

;

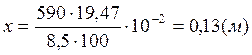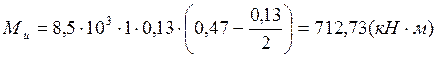
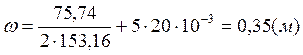
, поэтому принимаем место теоретического обрыва .

2) Для среднего пролёта:

Подсчитаем величину момента для 3Æ18A – IV:

;

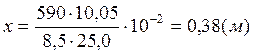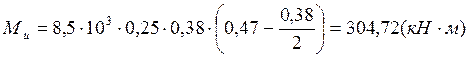
Так как расстояние от балки до теоретического места обрыва больше чем 0,25 пролёта то считаем с шагом S₂:

;

;

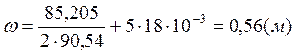, поэтому принимаем место теоретического обрыва .

4 Расчет и конструирование железобетонной колонны

4.1 Определение нагрузок и усилий в колоннах

Колонны рассматриваются как сжатый элемент со случайными эксцентриситетами. В состав нагрузок на колонну входят:

Постоянные – собственный вес конструкции перекрытия и колонны, а также слой грунта засыпки резервуара;

Временные – снеговая нагрузка согласно заданию на проектирование.

Собственный вес колонны определяется по предварительно назначенным размерам её поперечного сечения, которое имеет квадратную форму со сторонами .

Продольная сила в сечении колонны от полной расчётной нагрузки определяется по формуле:

,                                                                                (4.1.1)

где ,                                                                               (4.1.2)

где ;                                                                                              (4.1.3)

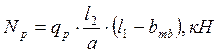;                                                                                    (4.1.4)

,                                                                                        (4.1.5)

где ,                                                           (4.1.6)

где  – объемный вес железобетона, ;

 – коэффициент надёжности равный 0,95;

 – коэффициент надёжности по нагрузке, равный 1,1.