Удаление из АВЛ-дерева происходит аналогично удалению из простого двоичного дерева, см. двоичные деревья. Пример: 4, 8, 6, 5, 2, 1, 7 из дерева на рис. 1
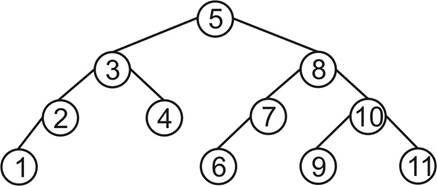
Рис. 1
Деревья оптимального поиска
Критерий сбалансированности: каждая страница (кроме корневой) должна содержать от n до 2n вершин. n – порядок Б-дерева.
Производительность поиска пропорциональна lognN.
Дополнительные правила:
• каждая страница либо представляет собой лист, либо имеет m+1 потомка, где m – количество ключей на данной странице.
• Все листья находятся на одном уровне.
Для правильной работы B-дерева необходимо, что бы на странице ссылки на следующий уровень были представлены в отсортированном виде. Поэтому для оптимизации операций вставки и удаления лучше использовать линейные списки.
Поиск в B-Дереве.
1. Если ki < x < ki+1 для i on 1 до m-1, то поиск продолжается на странице pi.
2. Если km < x, то поиск продолжается на странице pm.
3. Если k1 > x, то поиск продолжается на странице p0.
Включение в B-Дерево:
1. Ищется ключ. Если он не найден (или если допускается дублирование ключей), то производится попытка вставки на найденную страницу. Если страница содержит меньше 2n ключей, то ключ просто добавляется на эту страницу. Все добавления ключей происходят только в листьях! Если же на странице находится 2n ключей, то вставка не возможна и выполняется пункт 2.
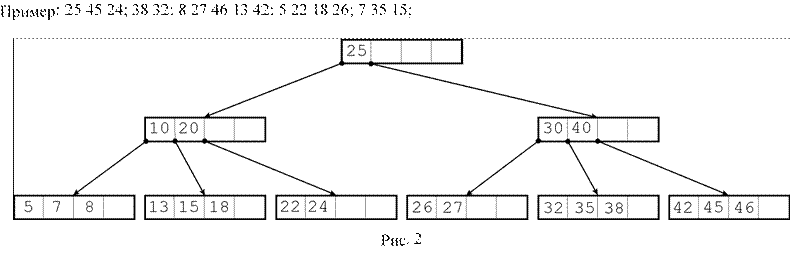
2. Заполненная страница разделяется на две одинаковых (в каждой будет по n элементов). Один средний ключ переносится на предыдущий уровень. Если предыдущий уровень также заполнен, то рекурсивно повторяется операция разделения для страницы предыдущего уровня. Пример:20; 40 10 30 15; 35 7 26 18 22; 5; 42 13 46 27 8 32 38 24 45 25;
Удаление из В-дерева.
1. Исключаемый элемент находится на листовой странице. Удаление очень простое.
2. Исключаемый элемент не на узловой странице. Заменить ближайшим лексикографическим смежным элементом (как для бинарного дерева).
3. Проверить, не нарушено ли условие сбалансированности. Если нарушено, то см. следующие пункты.
4. Попробовать выполнить балансировку страниц. Она состоит в том, что объединяется страница с нарушенной балансировкой и одна из соседних вместе с ключом, от которых они происходят. Далее элементы делятся поровну, а средний ключ заменяет родительский. Балансировка неудачна, если на соседней странице ровно n элементов. В этом случае необходимо выполнить слияние.
5. Слияние выполняется следующим образом. Обе страницы объединяются в одну с добавлением родительского ключа, а лишняя страница удаляется.
Функция распределения: H(k) = ORD(k) mod N, где H(k) – индекс в массиве для заданного ключа k, ORD – функция, преобразующая ключ в его порядковый номер во множестве всех возможных ключей, N – количество элементов массива, на которое делается отображение ключей (от 0 до N-1).
Требование к функции распределения: равномерное отображение значений ключей на весь диапазон индекса массива.
Разрешение конфликтов. Открытые и закрытые хэш-таблицы.
Линейные пробы H(k) = ORD(k+i) mod N, где i – номер пробы. Недостаток – группировка значений возле первичных ключей.
Квадратичные пробы H(k) = ORD(k+i2) mod N. Недостаток – просмотр не всех пустых элементов массива.
Удаление ключей – для открытой хэш-таблицы – просто удаление из списка; для закрытой – использование флагов – пустая или удаленная ячейка.
Среднее число попыток для линейных проб E=(1-a/2)/(1-a), где а – степень заполнения. Рекомендации – выделение большего количества элементов массива, чем необходимо, примерно на 10%. Если закрытая хэш-таблица заполнена более чем на 90% – создать новую хэш-таблицу вдвое большего размера и заполнить ее заново. Для открытой хэштаблицы критерием ее увеличения является K>= 2N, где К – количество сохраненных элементов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.