Информатика и выч. техника \ Прикладные системы искусственного интеллекта

Программа, которая считывает из входного файла функцию и выводит в выходной файл все корни функции. Проблема количества и положения корней, страница 2

* представляет собой вектор-столбец символических решений. К сожалению, в данной версии Matlab невозможно вывести в выходной файл эти решения. Кроме того, функцию solve компилятор отказывается переводить при создании exe-файла.

% M-файл find_all_roots_sym.m function find_all_roots_sym % Cчитываемизвходногофайлафункцию [FI,mes] = fopen('roots.in','rt'); F = fgetl(FI); fclose(FI); % Ивыводимкорнифункции r = solve(sym(F)); pretty(r);

Подведём итоги

Итак, пользователю всё равно нужно будет запускать Matlab и открывать M-файл. Пользователю было бы удобно, чтобы это делалось «за один раз». Т.е. решение системы нелинейных уравнений должно проходить в 2 этапа:

  1. Планирование расчёта в оболочке на Delphi. На выходе оболочка создает M-файл с описанием процесса решения задачи и вывода результатов.
  2. Загрузка M-файла в Matlab и исполнение его по клавише F5 с последующим просмотром результатов в окне Matlab.

Главное окно программы:

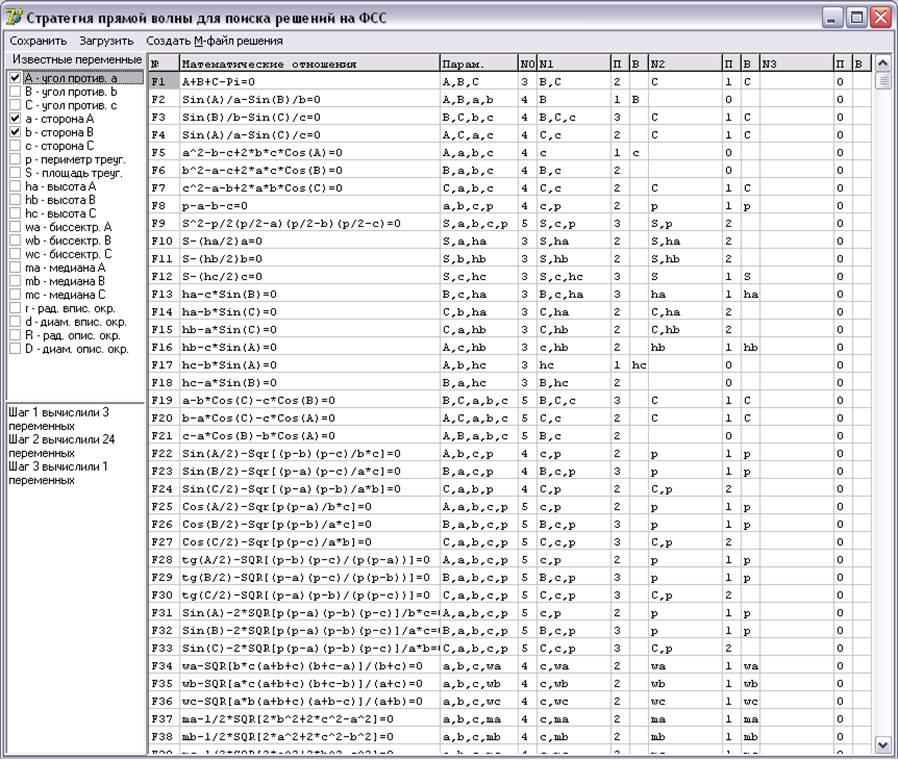
Для решения задачи следует в поле «известные переменные» отметить известные переменные. При каждом изменении таблица, содержащая план решения будет пересчитываться. В левом нижнем поле будет выводится количество переменных получаемых на каждом шаге вычислений.

Пример создания M-файла для предметной области «Квадрат»

Квадрат: S-площадь, a-сторона, diag-диагональ

F1    S-a^2=0

F2    2*a^2-diag^2=0

Для хранения описания формул и переменных предметной области был разработан простейший текстовый формат файла (для этого формата используется расширение .sem.). В первой строке файла записывается M-количество переменных. Далее идут M строк с описаниями переменных в формате:

<имя переменной> - <описание переменной>

Затем указано N-количество уравнений. Все уравнения должны быть в виде . Имя переменной должно состоять из букв и цифр, при этом на первой позиции обязательно должна быть буква.

Создадим описание предметной области «квадрат» в виде .sem файла в любом текстовом редакторе и сохраним файл под именем «квадрат.sem»:

3

S - площадь

a - сторона

diag - диагональ

2

S-a^2=0

2*a^2-diag^2=0

Выберем в главном окне программы пункт меню «Загрузить». При этом появится окно, как показано на рисунке:

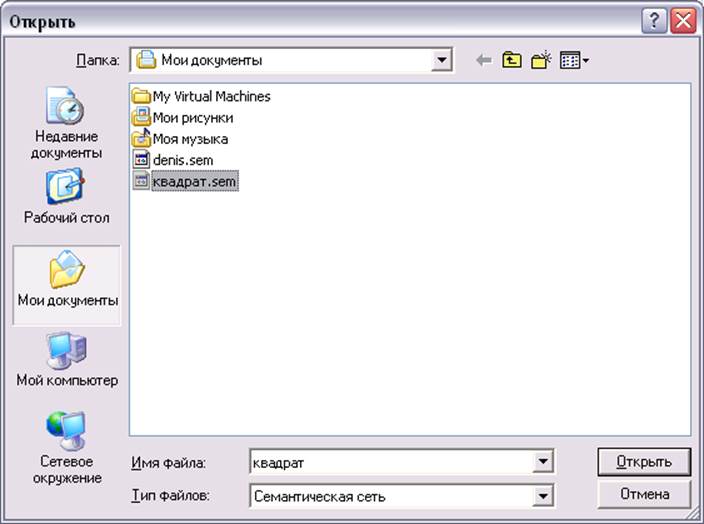
Выберем файл «квадрат.sem» и нажмём клавишу «Открыть». После успешного открытия файла появится окно, как показано на рисунке:

Нажмём клавишу «OK». В главном окне программы мы сможем просмотреть описание предметной области «квадрат». Вид главного окна программы показан на рисунке:

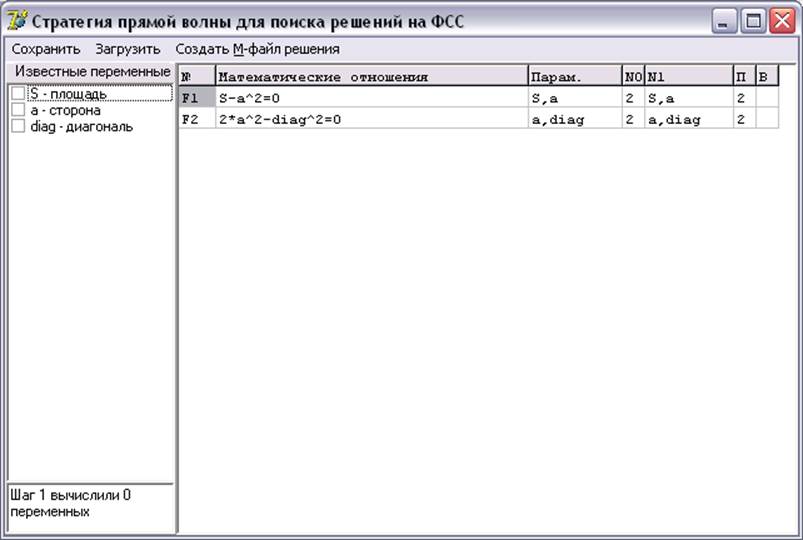
Т.к. ничего нельзя вычислить, алгоритм останавливается на первом шаге. Предположим, что нам известна площадь квадрата . Наведём на нёё правую курсор мыши и нажмём левую кнопку мыши. При этом будет создан план расчёта остальных переменных.

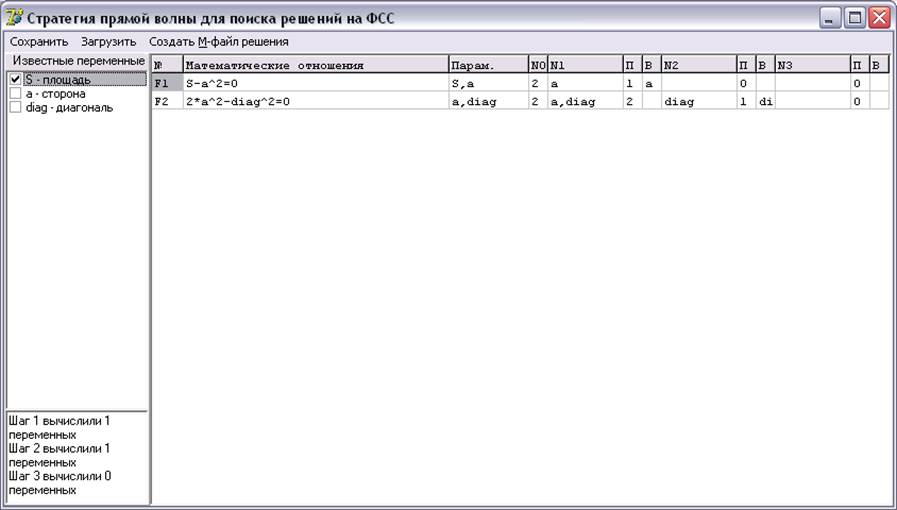
Мы видим, что сначала из первого уравнения можно вычислить сторону квадрата . А затем из второго уравнения – диагональ квадрата .

Выберем пункт меню «Создать M-файл решения». При этом появится окно, позволяющее выбрать имя для создаваемого файла.

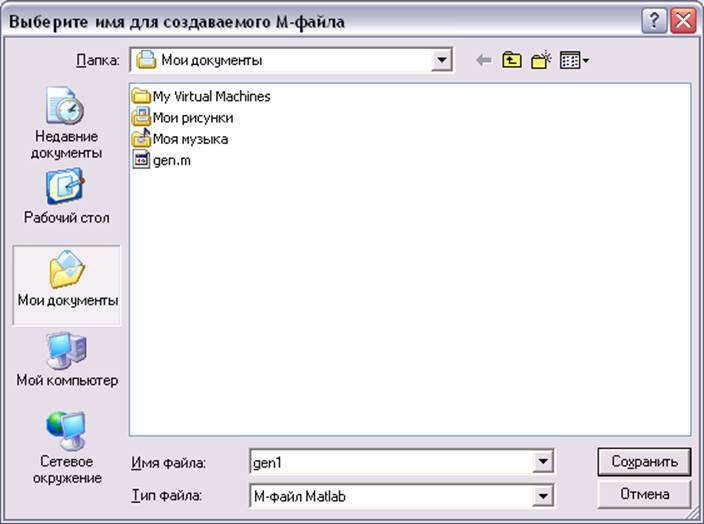
Выберите имя файла и нажмите «Сохранить». При успешном сохранении появится следующее окно:

Нажмите «OK». Теперь можно посмотреть содержимое созданного файла:

% Файл сгенерирован программой FSS.EXE

function gen1  % === Известные переменные === S = ; % Укажите значение S % === Вычисляем новую переменную 'a' === F = sym('S-a*a'); % Уравнение F1 % Подставляем известные переменные F = subs(F,'S',S); % Решаем систему и выводим ответ a = max(double(solve(F))); disp('a='); disp(a); % === Вычисляем новую переменную 'diag' === F = sym('2*a^2-diag^2'); % Уравнение F2 % Подставляем известные переменные F = subs(F,'a',a); % Решаем систему и выводим ответ diag = max(double(solve(F))); disp('diag='); disp(diag);

Следует заметить, что конкретное значение площади  не указано. Это сделано намеренно. Конкретное значение переменных можно поставить после открытия этого файла в Matlab. Можно также исследовать решения при различных значениях известных переменных.

Запустим Matlab и откроем полученный файл.

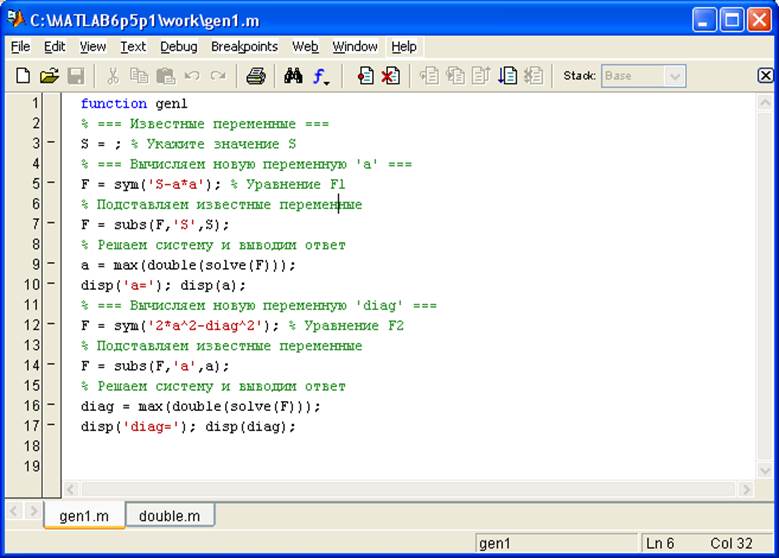
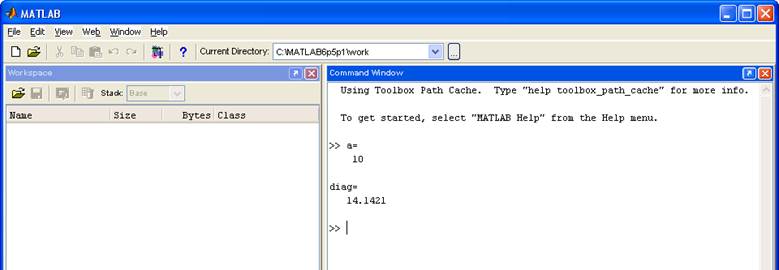
Указываем значение S=100. И запускаем программу на выполнение (F5).

В главном окне Matlab  появляется решение системы:

Скачать файл