использованием теоремы Колмогорова построить критерий значимости проверки простой гипотезы согласия с нормальным распределением с параметром λ0. Проверить гипотезу на уровне значимости α2. Вычислить наибольшее значение уровня значимости, на котором нет оснований отвергнуть данную гипотезу.
6. Используя гистограмму частот, построить критерий значимости χ2 проверки простой гипотезы согласия с нормальным распределением с параметром λ0. Проверить гипотезу на уровне значимости α2. Вычислить наибольшее значение уровня значимости, на котором ещё нет оснований отвергнуть эту гипотезу.
7. Построить критерий значимости χ2 проверки сложной гипотезы согласия с нормальным распределением. Проверить гипотезу на уровне значимости α2. Вычислить наибольшее значение уровня значимости, на котором ещё нет оснований отвергнуть эту гипотезу.
8. Построить наиболее мощный критерий проверки простой гипотезы о нормальности с параметрами λ = λ0 при альтернативе нормальности с параметрами λ = λ1. Проверить гипотезу на уровне значимости α2. Что получится, если поменять местами основную и альтернативную гипотезы?
9.
В пунктах
3-7 заменить семейство показательных распределений на семейство
гамма-распределений с плотностями 
.
1.1. Вариационный ряд.
|
xi |
0 |
1 |
2 |
3 |
5 |
6 |
8 |
|
ni |
29 |
9 |
6 |
2 |
2 |
1 |
1 |
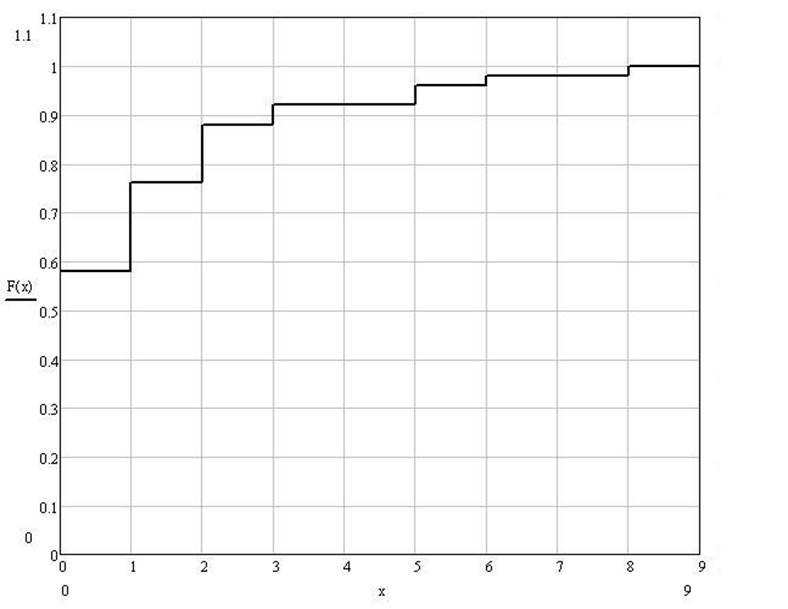
1.2. Эмпирическая функция распределения.
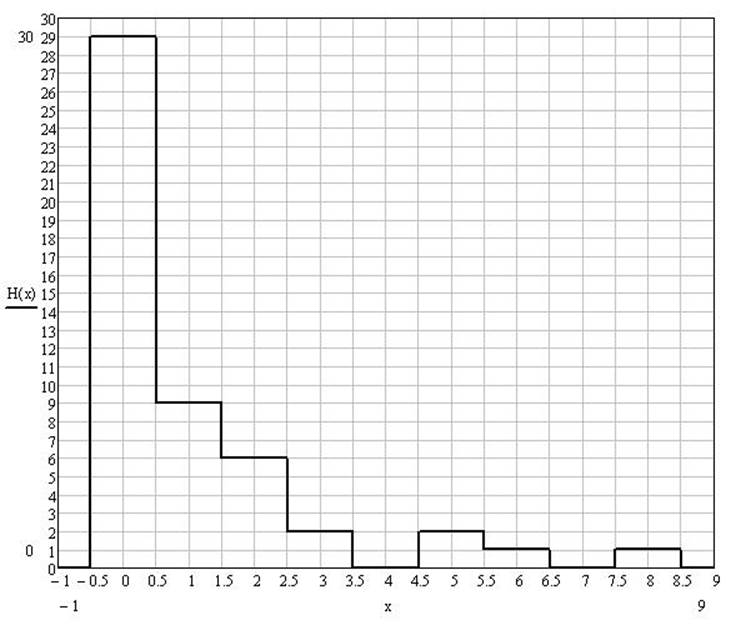
1.3.Гистограмма частот.
2.1. Математическое ожидание.
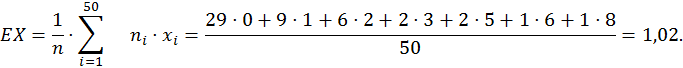
2.2. Дисперсия.
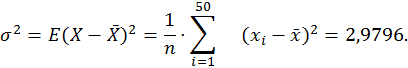
2.3. Медиана.
2.4. Ассиметрия.
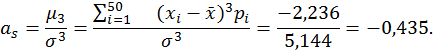
2.5. Эксцесс.
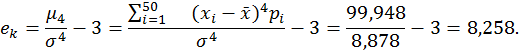
2.6. Вероятность попадания в [a, b].
3.1. Оценка максимального правдоподобия параметра λ.
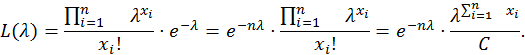
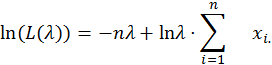
Смещение:
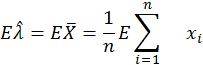
оценка несмещённая.
3.2. Оценка λ по методу моментов.
оценка несмещённая.
4. Асимптотический доверительный интервал уровня значимости α1 = 0,02 для параметра λ на базе оценки максимального правдоподобия.
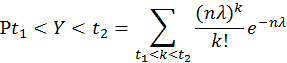
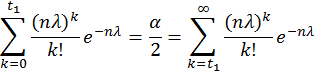
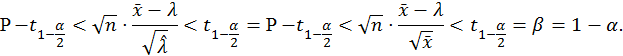
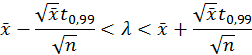
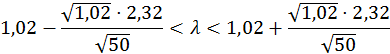
5. Построение критерия значимости χ2 проверки простой гипотезы согласия с распределением Пуассона с параметром λ0 = 3,0 на основе гистограммы частот. Проверка гипотезы на уровне значимости α1 = 0,02. Вычисление наибольшего значения уровня значимости, на котором ещё нет оснований отвергнуть гипотезу.
, 
.
, 
.
, 
.
, 
.
.
.
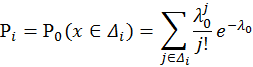
гипотезу отвергаем.
Наибольшее значение уровня значимости, при котором ещё нет оснований отвергнуть данную гипотезу, очень мало (<< 0.01). .
6. Построение критерия значимости χ2 проверки сложной гипотезы согласия с распределением Пуассона. Проверка гипотезы на уровне значимости α1 = 0,02. Вычисление наибольшего значения уровня значимости, на котором ещё нет оснований отвергнуть гипотезу.
, 
.
, 
.
, 
.
, 
.
.
.
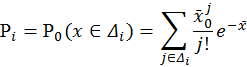
гипотезу отвергаем.
Наибольшее значение уровня значимости, при котором ещё нет оснований отвергнуть данную гипотезу, очень мало (<< 0.01) .
7. Построение наиболее мощного критерия проверки простой гипотезы пуассоновости с параметром λ0 = 3,0 при альтернативе пуассоновости с параметром λ1 = 1,0. Проверка гипотезы на уровне значимости α1 = 0,02. Получение результата при условии, что основная и альтернативная гипотезы были поменяны местами.
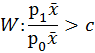
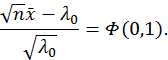
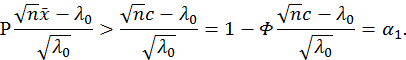
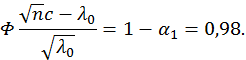
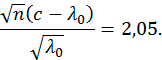
гипотезу отвергаем.
При изменении мест основной и альтернативной гипотез произойдёт следующее:
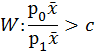
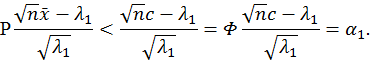
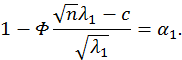
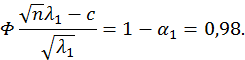
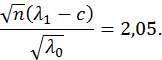
гипотезу отвергаем.
8. Заменим семейство распределений Пуассона
на семейство геометрических распределений 
8.1.1. Оценка максимального правдоподобия параметра λ.
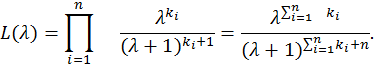
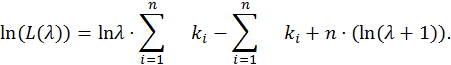
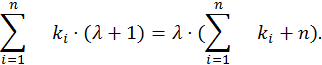
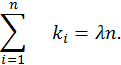
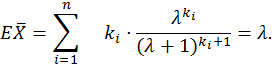
Смещение:
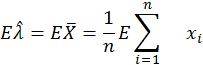
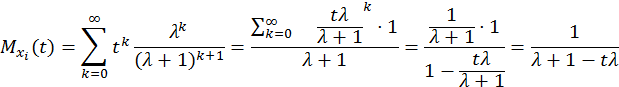
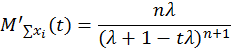
оценка несмещённая.
8.1.2. Оценка λ по методу моментов.
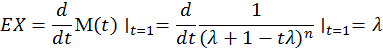
оценка несмещённая.
8.2. Асимптотический доверительный интервал уровня значимости α1 = 0,02 для параметра λ на базе оценки максимального правдоподобия.
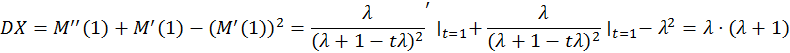
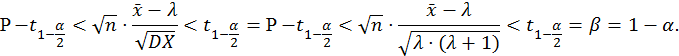
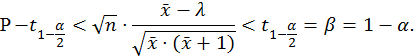
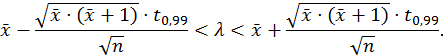
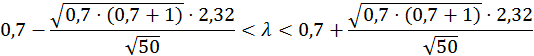
8.3. Построение критерия значимости χ2 проверки простой гипотезы согласия с геометрическим распределением с параметром λ0 = 3,0 на основе гистограммы частот. Проверка гипотезы на уровне значимости α1 = 0,02. Вычисление наибольшего значения уровня значимости, на котором ещё нет оснований отвергнуть гипотезу.
, 
.
, 
.
, 
.
, 
.
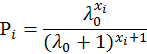
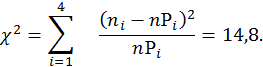
гипотезу отвергаем.
Наибольшее значение уровня значимости, при котором ещё нет оснований отвергнуть данную гипотезу, очень мало (<< 0,01).
8.4. Построение критерия значимости χ2 проверки сложной гипотезы согласия с геометрическим распределением. Проверка гипотезы на уровне значимости α1 = 0,02. Вычисление наибольшего значения уровня значимости, на котором ещё нет оснований отвергнуть гипотезу.
, 
.
, 
.
, 
.
, 
.
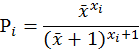
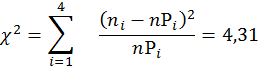
гипотезу принимаем.
Наибольшее значение уровня значимости, при котором ещё нет оснований отвергнуть данную гипотезу, примерно равно 0,12.
1.1. Вариационный ряд.
|
№ |
Значение |
№ |
Значение |
№ |
Значение |
№ |
Значение |
№ |
Значение |
|
1 |
0,00 |
11 |
0,07 |
21 |
0,40 |
31 |
1,23 |
41 |
3,29 |
|
2 |
0,00 |
12 |
0,08 |
22 |
0,43 |
32 |
1,24 |
42 |
3,60 |
|
3 |
0,00 |
13 |
0,08 |
23 |
0,61 |
33 |
1,48 |
43 |
3,86 |
|
4 |
0,01 |
14 |
0,11 |
24 |
0,64 |
34 |
1,58 |
44 |
4,20 |
|
5 |
0,01 |
15 |
0,14 |
25 |
0,82 |
35 |
1,80 |
45 |
6,20 |
|
6 |
0,02 |
16 |
0,17 |
26 |
0,84 |
36 |
1,85 |
46 |
6,93 |
|
7 |
0,03 |
17 |
0,20 |
27 |
0,87 |
37 |
1,89 |
47 |
7,88 |
|
8 |
0,04 |
18 |
0,27 |
28 |
0,92 |
38 |
2,15 |
48 |
8,72 |
|
9 |
0,04 |
19 |
0,33 |
29 |
0,95 |
39 |
2,55 |
49 |
9,11 |
|
10 |
0,07 |
20 |
0,39 |
30 |
0,96 |
40 |
3,12 |
50 |
13,02 |
1.2. Эмпирическая функция распределения.
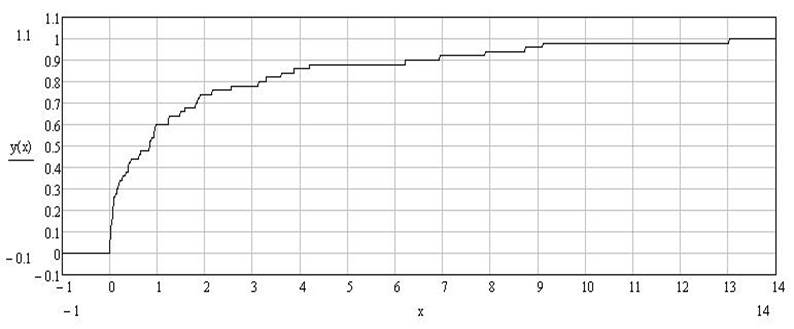
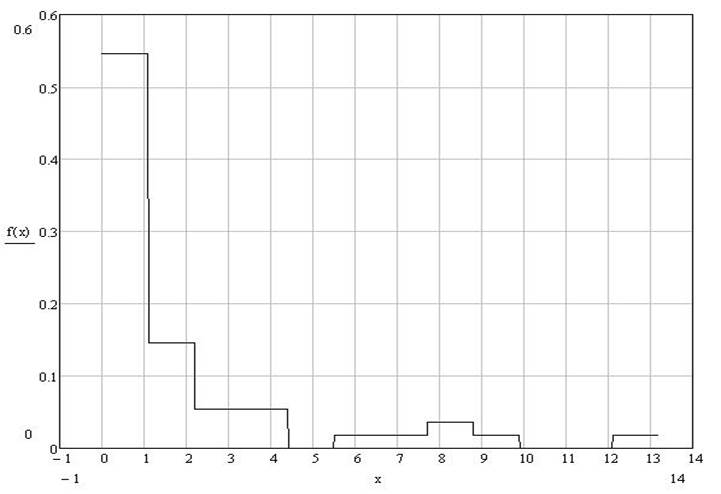
1.3. Гистограмма частот и полигон частот
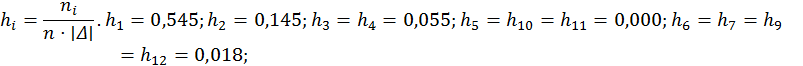
2.1. Математическое ожидание.
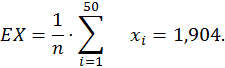
2.2. Дисперсия.
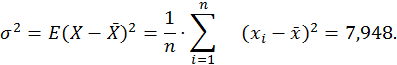
2.3. Медиана.
2.4. Ассиметрия.
2.5. Эксцесс.
2.6. Вероятность попадания в [a, b].
3.1. Оценка максимального правдоподобия параметра λ .
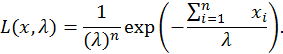
- оценка
несмещённая.
3.2. Оценка параметра λ по методу моментов.
- несмещённая.
4. Построение доверительного интервала уровня значимости α2 = 0,2 для параметра λ. Используем преобразование Смирнова
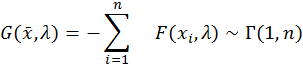
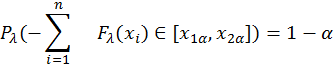
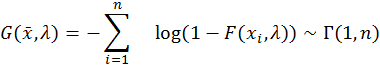
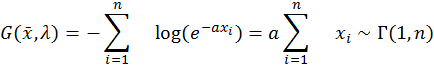
Доверительный интервал:
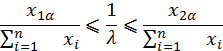
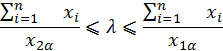
5. Построение критерия значимости проверки простой гипотезы согласия с нормальным распределением с параметром λ0 с использованием теоремы Колмогорова. Проверка гипотезы на уровне значимости α2 = 0,2. Вычисление наименьшее значения уровня значимости, на котором
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.