Обработка результатов прямых измерений. Обработка результатов косвенных измерений. Определение погрешностей электроизмерительных приборов. Расчёт измерительных преобразователей токов и напряжений. Расчёт измерительных цепей с использованием трансформаторов тока и напряжений

среднеарифметическое отклонение каждого отдельного наблюдения.

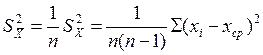                                                 (1.1)

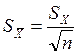-среднеквадратическое отклонение величены Х_ср.

Итог измерения записывается в виде

                                                                   (1.2)

                                                                    (1.3)

t_p-коэффициент Стьюдента (зависит от числа наблюдений n и доверительной вероятности Р)

Задача 1

Произведено 12 измерений емкости конденсатора, давших значения емкости, приведенные в таблице 1.1.

Таблица 1.1 - Результаты измерений ёмкости конденсатора.

Определить с доверительной вероятностью Р=0,95 интервал, в котором находится значение измеряемой емкости.

Для n=12, Р=0,95, t_р=2,18.

При проведении расчетов целесообразно сводить промежуточные результаты в таблицу вида:

Таблица 1.2 - Результаты расчётов.

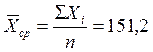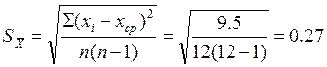пФ;

пФ;

пФ

пФ

Следовательно:

C=151,2+2,18/0,27=(151+0.59)пФ

Задачи 2,3,4 решаются по карточкам заданиям с изменением исходных данных.

Задача 2

Произведен ряд независимых наблюдений напряжения.

Таблица 1.3 - Результаты измерения напряжения.

Предполагая, что систематической погрешностью можно пренебречь, определите оценку истинного значения измеряемого напряжения U и среднеквадратические погрешности методы измерения S_х и результаты измерения S_х.

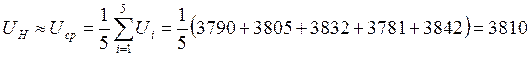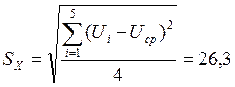мВ

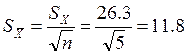мВ

мВ

Задача 3

Цифровым вольтметром постоянного тока выполнена серия прямых равноточных измерений напряжения. Обработать результаты этих измерений, если n=15 p=0.95. Закон распределения результатов нормальный.

Таблица 1.4 - Данные для расчета.

Задача 4

Обработать результаты наблюдений, полученные при измерении ускорения свободного падения. Распределение результатов считать нормальным, доверительную вероятность принять равной 0,95.

Таблица 1.5 - Данные для расчёта.

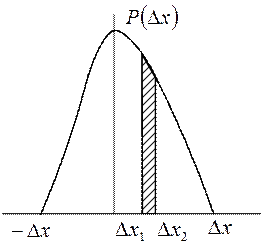Любая величина имеет отклонение от истинного значения, и эти отклонения существуют по теории вероятности, чем больше ошибка, тем меньше вероятность ее проявления.

Рисунок 1.2 - Нормальный закон распределения.

2. Практическое занятие №2, 3

Тема: Обработка результатов косвенных измерений.

Цель: Освоить методику математической обработки результатов косвенных измерений.

Если случайная величина Y cвязана с независимыми случайными величинами Y₁;Y₂      Y_n известной функциональной зависимостью Y=F(Y₁,Y₂     Yn), то зная математические ожидания m_y1; m_y2    m_yn  и среднеквадратические отклонения S_y1 , S_y2     S_n  величин Y₁ Y₂    Y_n можно приближенно найти математическое ожидание m_y и среднеквадратическое отклонение S_y величину Y по формуле: (Y=F(Y₁,Y₂     Yn).

Пусть Y₁ Y₂      Y_n –случайные результаты прямых независимых измерений различных физических величин, а Y=F(Y₁,Y₂     Yn)-результат косвенного измерения.

Тогда среднеквадратическое отклонение S_y случайной погрешности результата косвенного измерения можно найти по формуле 2.1:

m_y=F(m_y1;m_y2;…m_yn)                                                               (2.1)

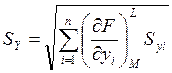,                                                               (2.2), где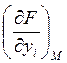- чистая производная функции F(y₁,y₂…y_n) по y_i, ,взятая в точке (m_y1,m_y2…m_yn).

Пусть Y₁,Y₂,…Y_n-случайные результаты прямых независимых измерений различных физических величин, а Y=(Y₁,Y₂…Y_n)-результат косвенного измерения.

Тогда среднеквадратическое отклонение S_y. Случайной погрешности результата косвенного измерения можно найти по формуле: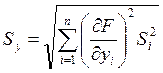, где S_i –среднеквадратическое отклонение случайной погрешности результата прямого измерения Y_i, а частная производная берется в точке

у₁ у₂    у_n.

Соответствующей результатом прямых измерений.

Задача 1

Сопротивление R составлено из параллельно включенных сопротивлений R₁ и R₂, математические ожидания и среднеквадратические отклонения которых известны: m₁=12Ом; m₂ =15Ом; S₁=1Ом; S₂ =0,5Ом.

Найдите математические ожидания mR и среднеквадратическую погрешность S₁₂,сопротивление R.

Решение.

При параллельном соединении:.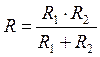

Воспользуемся формулами (2.1) и (2.2), тогда: 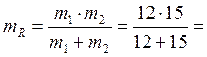6.67 Ом

Для нахождения S_R вычисляем сначала частные производные:

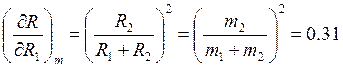
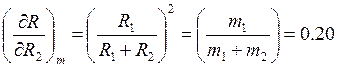
Далее получи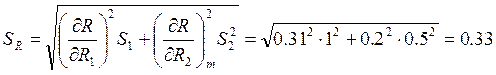м: Ом

Задача 2

Известны математические ожидания и среднеквадратические отклонения сопротивлений R₁ и R₂; m₁=10Ом; m₂=20Ом; S₁=0,10Ом; S₂=0,14. Найдите математическое ожидание и среднеквадратические отклонения отношения сопротивлений последовательного соединения R1 и R2 и параллельного.

Данные для разных вариантов помещены в таблицу 2.1

Таблица 2.1 - Данные для разных вариантов.

Задача 3

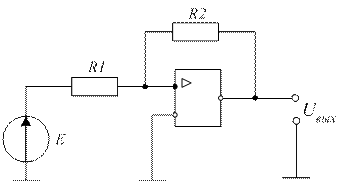
Измерительный усилитель построен на базе операционного усилителя путем применения параллельной отрицательной обратной связи по напряжению. Математическое ожидание и среднеквадратическое отклонение сопротивлений R1 и R2 цепи отрицательной обратной связи известны:

m₁ =1кOм; m₂=10кОм; S₁=1Oм; S₂=10Oм.

Определите математическое ожидание m_k и среднеквадратическое отклонение S_к коэффициента усиления.

К-коэффициент усиления по напряжению измерительного усилителя: .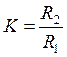

Рисунок 2.1 - Измерительный усилитель.

Таблица 2.2 - Варианты заданий.

Задача 4

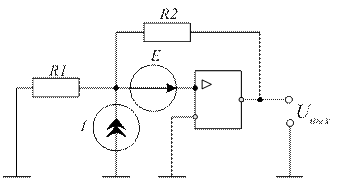Измерительный усилитель построен по схеме, изображенной на рисунке 2.2. Этот операционный усилитель имеет дрейф нуля. Известны математические ожидания и среднеквадратические отклонения выходных параметров источника тока и ЭДС, определяющих дрейф (значения). Определите математическое ожидание m и среднеквадратические