Схема привода цепного конвейера с двухступенчатым цилиндрическим редуктором. Параметры кинематического расчета

ЗАДАНИЕ

НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

ЗАДАНИЕ №1.5, ВАРИАНТ №2.

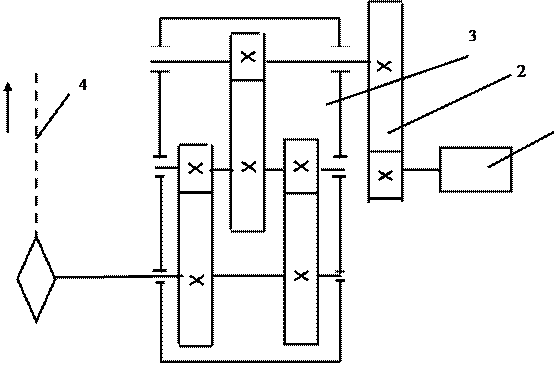
1 – электродвигатель; 2 – цилиндрическая  передача; 3 – двухступенчатый цилиндрический редуктор редуктор; 4-тяговая цепь.

				1

 

Рисунок 1 – Схема привода цепного конвейера с двухступенчатым цилиндрическим редуктором.

Таблица 1 – Заданные параметры курсового проектирования.

1 Кинематический расчет                                                                                                        

1.1 Данные для расчёта

мм

1.2 Выбор электродвигателя

Определяем выходную мощность двигателя:

                                                                                 (1.1)

кВт

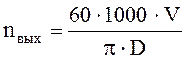
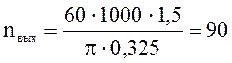об/мин                                                   (1.2)

                                                       (1.3)

где   коэффициент полезного действия привода

 КПД открытой передачи;

 КПД цилиндрической передачи;

КПД пары подшипников.

1.3 Определяем требуемую мощность двигателя

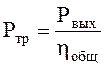                                                                                                                                                             (1.4)                            

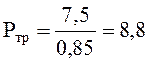 кВт

В результате расчета мы пришли к тому, что требуемый двигатель должен иметь мощность не менее 8,8 кВт и наибольшим количеством оборотов. Электродвигатель наиболее подходящий к этим требованиям – 132М5/2900. Основные параметры

 кВт    об/мин

1.4 Определяем общее передаточное число

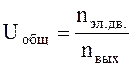                                                                                                    (1.5)   

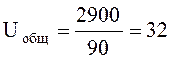
где передаточное число открытой передачи;

 передаточное число закрытой косозубой передачи;

 передаточное число закрытой прямозубой передачи;    (1.6)

 

1.5 Определяем силовые и скоростные параметры на валах

Определяем мощности на валах

                                                             (1.7)

 кВт

                                                                                      (1.8)

 кВт

                                                                     (1.9)

 кВт

Определяем обороты на каждом валу:

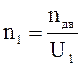                                                                                                                                                          (1.10) (1.11)

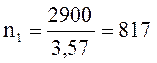
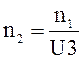                                                                                     (1.12)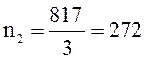

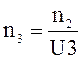
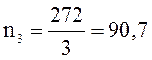
Определяем угловую скорость на каждом валу привода:

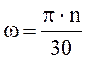                                                                                    (1.13)

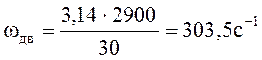
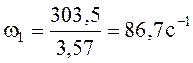
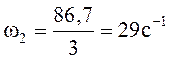
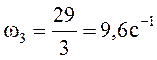
Определяем крутящий момент на валах привода:

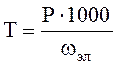                                                                                                                                                                                                          (1.14)                     

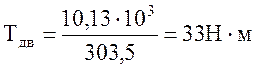
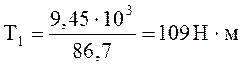
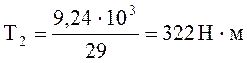
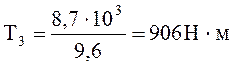
Таблица 1. Параметры кинематического расчета

№ вала	Р, кВт	n, об/мин	ω, с-1	Т, Н*м	i
0	10,13	2900	303,5	33	3,57
1	9,75	817	86,7	109
					3
2	9,34	272	29	322
					3
3	8,7	90,7	9,6	906

2 Расчет закрытой цилиндрической косозубой передачи

2.1 Выбор материала и расчёт допускаемых напряжений

Для равномерного изнашивания зубьев и лучшей их прерабатываемости твердость шестерни выбирается больше твердости колеса: .

И для шестерни, и для колеса выбираем сталь 45 с термообработкой - улучшение, ,  

,                                                                         (2.1)     

где предел контактной выносливости при базовом числе циклов;

коэффициент долговечности;

Для колеса -

Для шестерни -

Находим допускаемые контактные напряжения и напряжения изгиба

[4, таблица 2.2]:

Допускаемое контактное напряжение для шестерни:

                                                                    (2.2)

Для колеса

Расчет ведется по меньшему значению

Допускаемое напряжение на изгиб:

,                                                                        (2.3)

где   предел выносливости материала при нулевом цикле изгиба   [1, стр.36].

Допускаемое напряжение на изгиб для шестерни:

Допускаемое напряжение на изгиб для колеса:

 

2.2 Предварительный расчёт передачи

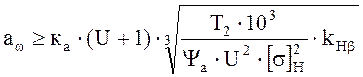                                        (2.4)

где коэффициент распределения нагрузки по длине зуба;

коэффициент ширины венца колеса и вспомогательный коэффициент соответственно для прямозубых передач

Принимаем: [1, таблица 2.3], [4, стр. 13],

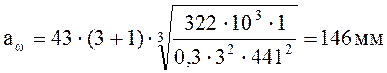
Принимаем ближайшее значение по ГОСТу .

Выбираем модуль зацепления в интервале:                                                                                                               

                                                                                                              (2,5)

Принимаем m=2,8

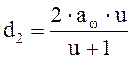                                                                                                              (2,6)

мм

                                                                                                              (2,7)

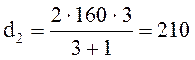мм

Определяем угол наклона зубьев  

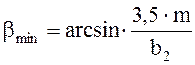                                                                                                              (2,8)

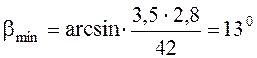
Определяем число зубьев ступени:

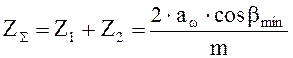                                                    (2.9)

   

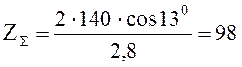
Определяем число зубьев шестерни

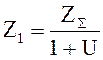                                                                                  (2.10)

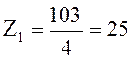
Определяем число зубьев колеса

                                                                                                            (2,11)

Определяем фактическое передаточное число:

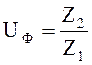                                                                                                                                                                    (2.12)

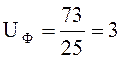
Определяем основные размеры зубчатых колёс:

Делительные диаметры колес:

                                                                                                            (2.13)           

мм

мм

Диаметры окружностей вершин и впадин шестерни и колеса:

                                                                                                                                                                (2.14)

                                                                            (2.15)   

Ширины шестерни и колеса:

                                                                                                            (2.16)

мм

Определяем силы в зацеплении:

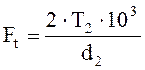                                                                                                            (2.17)

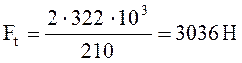
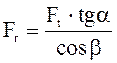
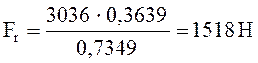                                                                            (2.18)

                                                                                                   (2.19)

2.3 Проверочный расчёт передачи

Действительное контактное напряжение:

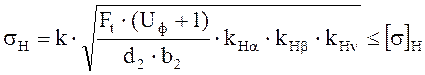,                            (2.20)

где вспомогательный коэффициент

,                                                                   (2.21)       

где коэффициент, учитывающий распределение нагрузки между зубьями;

коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи.

Принимаем: ,  [2, стр.16]

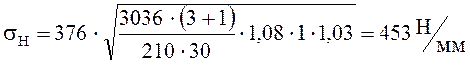
Погрешность контактного напряжения:

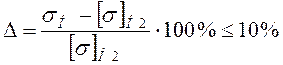                 (2.22) 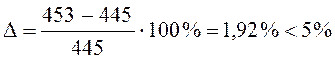        такая перегрузка допустима

Действительное напряжение от изгиба

Расчет действительного напряжения от изгиба зубьев ведется по колесу как наиболее слабому звену в передаче.

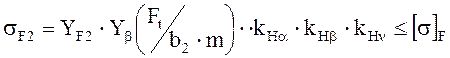,                       (2.23)

где коэффициент формы зуба;

коэффициент нагрузки.

Принимаем: ,  [2, стр.18]

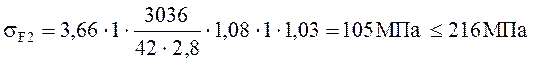
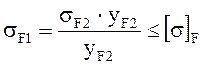
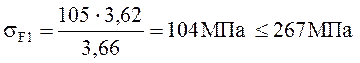
При проверочном расчете напряжения от изгиба меньше допускаемого, т.к. нагрузочная способность большинства зубчатых передач ограничивается Контактной прочность

3 Расчет закрытой прямозубой передачи

3.1 Выбор материала и расчёт допускаемых напряжений

Для равномерного изнашивания зубьев и лучшей их прерабатываемости твердость шестерни выбирается больше твердости колеса: .

И для шестерни, и для колеса выбираем сталь 45 с термообработкой - улучшение, ,  

,                                                                         (3.1)     

где предел контактной выносливости при базовом числе циклов;

коэффициент долговечности;

Для колеса -

Для шестерни -

Находим допускаемые контактные напряжения и напряжения изгиба

[4, таблица 2.2]:

Допускаемое контактное напряжение для шестерни:

                                                                    (3.2)

Для колеса

Расчет ведется по меньшему значению

Допускаемое напряжение на изгиб:

,                                                                        (3.3)

где   предел выносливости материала при нулевом цикле изгиба   [1, стр.36].

Допускаемое напряжение на изгиб для шестерни:

Допускаемое напряжение на изгиб для колеса:

3.2 Предварительный расчёт передачи

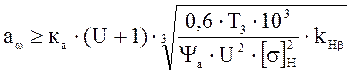                                           (3.4)

где коэффициент распределения нагрузки по длине зуба;

коэффициент ширины венца колеса и вспомогательный коэффициент соответственно для прямозубых передач

Принимаем: [1, таблица 2.3], [4, стр. 13],

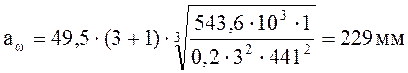
Принимаем ближайшее значение по ГОСТу .

Выбираем модуль зацепления в интервале:                                                                                                               

                                                                                                              (3,5)

Принимаем m=5

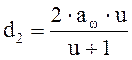                                                                                                              (3,6)

мм

                                                                                                              (3,7)

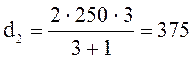мм

Определяем число зубьев ступени:

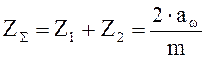                                                                  (3.8)

   

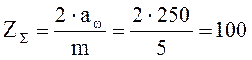
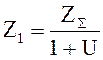                                                                                    (3.9)

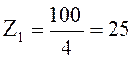
Определяем фактическое передаточное число:

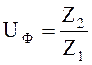                                                                                                                                                                    (3.10)

Определяем основные размеры зубчатых колёс:

Делительные диаметры колес:

                                                                                                                                                                                    (3.11)           

мм

мм

Диаметры окружностей вершин и впадин шестерни и колеса:

                                                                                                                       (3,12)

                                                                      

                                                                                                                             (3.13)                                                                                                           

Ширины шестерни и колеса:

                                                                                                            (3,14)

мм

Определяем силы в зацеплении:

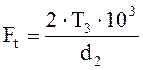                                                                                                            (3,15)

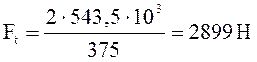
                                                                                                    (3.16)

3.3 Проверочный расчёт передачи

Действительное контактное напряжение:

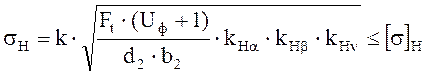,                            (3.17)

где вспомогательный коэффициент

,                                                                   (3.18)       

где коэффициент, учитывающий распределение нагрузки между зубьями;

коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи.

Принимаем: ,  [2, стр.16]

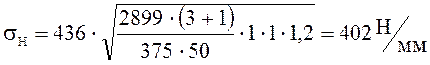
Погрешность контактного напряжения:

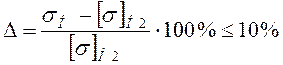                 (3.19) 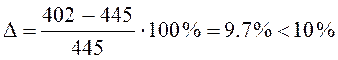         такая недогрузка допустима

Действительное напряжение от изгиба

Расчет действительного напряжения от изгиба зубьев ведется по колесу как наиболее слабому звену в передаче.

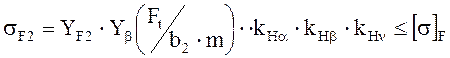,                       (3.20)

где коэффициент формы зуба;

коэффициент нагрузки.

Принимаем: ,  [2, стр.18]

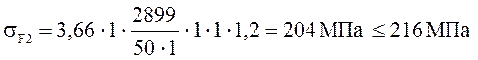
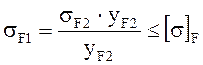                                                                                                            (3.21)

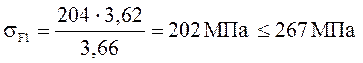
При проверочном расчете напряжения от изгиба значительно меньше допускаемого, т.к. нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью

4 Расчет открытой цилиндрической прямозубой передачи

4.1 Выбор материала и расчёт допускаемых напряжений

Для равномерного изнашивания зубьев и лучшей их прерабатываемости твердость шестерни выбирается больше твердости колеса: .

Принимаем для шестерни сталь 45 улучшенную до средней твердости НВ=208.Для колеса принимаем сталь 45,улучшенную до средней твердости НВ=186,  

4.2Определяем  контактные напряжения и напряжение на изгиб:

,                                                                                                               (4.1)

коэффициент долговечности;                                                                                                                                                         где   предел выносливости материала при нулевом цикле изгиба   [1, стр.36].

Допускаемое напряжение на изгиб для шестерни:

Допускаемое напряжение на изгиб для колеса:

 

Расчет ведется по меньшему значению

Допускаемое контактное напряжение для шестерни:

                                                                          

Для колеса

Расчет ведется по меньшему значению

Принимаем число зубьев шестерни согласно рекомендациям