адиабата расширения пара в цилиндре паровой машины, вторая—
адиабата сжатия пароводяной смеси в компрессоре.
Построим теперь для тех же значений температур ^ и ^ Дчз'
грамму цикла Ренкина. Это построение начнем с состояния виды, уже доведенной до начала кипения и имеющей температуру ^
(точка 4). От этой точки процесс пойдет сначала так же, как и в цикле Карно, т. е. по изотерме (и изобаре) 4-1, а затем по адиабате 1-2. Дальнейшее протекание этого цикла будет уже отличаться от цикла Карно. В последнем, как известно, процесс конденсации не доводится до конца, а заканчивается в точке 3, после чего сжатием по адиабате 3-4 смесь пара с конденсатом превращается целиком в жидкость, имеющую температуру ^, и в этом состоянии подается в котел (точка 4).
В цикле же Ренкина пар конденсируется полностью в воду, а поэтому линия этого процесса должна дойти до точки 5, лежащей на кривой жидкости при температуре ^- При этой температуре вода нагнетается в паровой котел, где подогревается до температуры ^ (точка 4). Процесс подогрева воды изобразится на диаграмме линией 5-4.
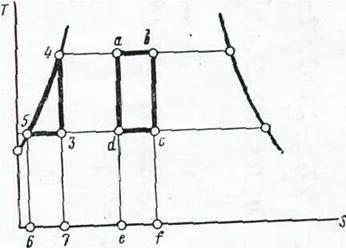
Сопоставляя диаграммы 1-2-3-4 и 1-2-5-4,
видим, что в цикле Карно.
вода подается в паровой котел уже подогретой до температуры ^, в цикле же Ренкина вода подается в котел „холодной" при температуре ^ (точка 5) и нагревается в нем при постоянном давлении до температуры ^. Теплота, затрачиваемая на нагрев, определяется нд диаграмме площадью
6-5-4-3-7, теплота, переводимая в полезную работу — площадью 5-4-3,
а отдаваемая в холодильник — площадью 6-5-3-7.
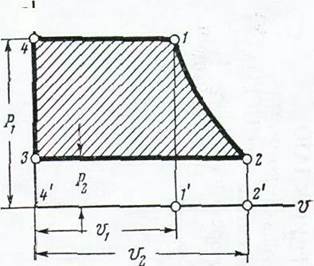
Рис. 108. К объяснению, почему цикл Ренкина
менее экономичен, чем цикл Карно', при одина-
ковых перепадах температур ^
В цикле Карно такому же количеству теплоты, отданной холодильнику, соответствует большее количество теплоты, превращенной в работу. Сказанное поясняется рис. 108, на котором сопоставлены часть диаграммы цикла Ренкина, относящаяся к процессу подогрева воды в паровом котле от температуры ^ ДО ^ (цифровые обозначения те же, что и на рис. 107), и диаграмма цикла Карно аЬсй,
построенная для того же перепада температур и при одинаковых количествах теплоты, отданной в холодильнике (площадь 5-3-7-6-
площади с1с/е). Как видим, при этих условиях площадь 5-4-3 меньше пло щади аЬсй, из чего следует, что подвод теплоты по изобаре 5-4
менее экономичен, чем по изотерме — изобаре аЬ.
Менее экономичное использование теплоты, подводимой в цикле
Ренкина на участке 5-4, делает этот цикл в целом менее экономичным, чем цикл Карно.
ЦИКЛА гдмкиид.
Для нахождения величины работы 1 кг пара в цикле Ренкина воспользуемся рис. 109, на котором изображена -иР-диаграмма этогоцикла. Площадь диаграммы 1-2-3-4 представляет в некотором масштабе величину искомой I
нами работы. Как видно *| "
из рассматриваемого рисунка, площадь 1-2-3-4 ==
==площади ]-1'-4'-4-\-\1ло-
щадь 1-2-2''-Г—площадь
2-2'-4'-3.
Имея в виду, что площадь 1-2-3-4 = /о; площадь 1-1'-4'-4 == Р^\; площадь 1-2-2-'-Г =/^==427 (»! — Ну) и площадь
2-2'-4'-3 = Р-^г, можем написать, что:
/о=Р^1+427(К1-й,).
Рис. 109. К выводу формул для полезной
работы в цикле Ренкина
— ?2^2 КГМ/КГ.
Перегруппировывая члены правой части этого уравнения, получим
^о=(427й1+Р^^1)-(427»2+^2) кгм/кг.
Вынесем величину 427 за скобки:
/, == 427 (и, + й-7 р^ ) - 427 ("2 + 4^7 р^ ) =
= 427 («I + АР^г) - 427 (гг, + АР^).
Величины, стоящие в скобках, являются энтальпиями ^ и ^.
Поэтому
/л=427г,-427(, или окончательно
/0=427^-?:,). (97>
Из этого уравнения видно, что величина полезной работы в цикле
Ренкина находится в прямой пропорциональной зависимости от разности энтальпий г\ — ^. Эта разность называется теплопадением или тепловым напор ом.
Как видим, величину работы, совершаемой 1 кг пара в цикле
Ренкина, можно легко подсчитать по хг-диаграмме. Зная, что
270000 / ,^ ^
й== —,—— (см. цикл Карно), подсчитаем расход пара для цикла'о
249
"Ренкина. Подставляя в это уравнение значение /д из уравнения (86), получим
. 270000
<1=-.
- 427 (Л-/,)
;или
а=^
632
'1— 11
КГ/Л. С. Ч.
(98)
Термический к. п. д. любого обратимого цикла, как известно,
•может быть выражен уравнением (45);
^ Л/о.
" II '
В частности, для цикла
Ренкина согласно уравнению (97)
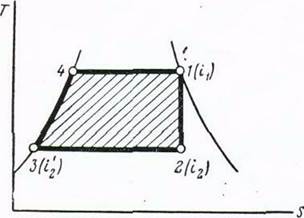
А1ц == <1 — 4 ккал/кг.
Здесь ^—энтальпия пара в точке 1, а г'2 — в точке 2
(рис. 110). Теплоту д^, подводимую на участке диаграммы 3-4-1, можно найти как разность энтальпий в конечной и начальной точках этого участка диаграммы. Таким образом,
Рис. 110. К нахождению величины работы
••пара и термического к. п. д. в цикле Ренкина
1^ — г/ ккал/ кг,
^1 = 1^ — ц ккал/ кг, где:
(\ — начальная энтальпия пара;
г/ — энтальпия воды при температуре 1ц, в холодильнике.
Подставляя значения Л/д и ^ в уравнение для •»](, получим уравнение для термического к. п. д. цикла Ренкина:
Чг
(99)
Расчет состояния системы в четырёх основных точках цикла.
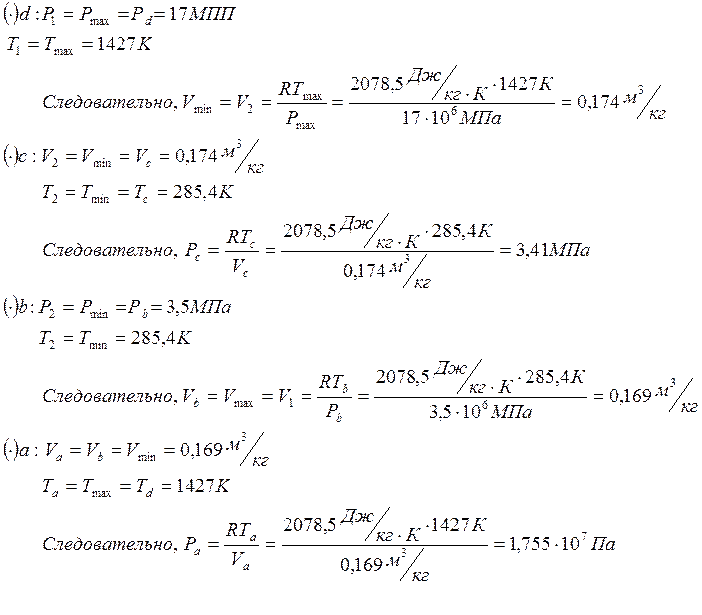
Проверка:
Так как процесс d-a изотермический, то
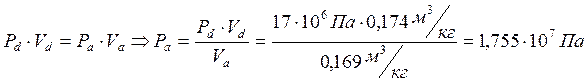
Процесс a-b изохорический, следовательно
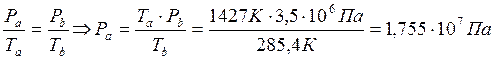
Из проверки следует, что расчёт выполнен верно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.