Методы прикладной статистики. Случайная величина, ее распределения и характеристики. Дифференциальная и интегральная функции распределения

задача решается на таком материале, где эти прочие аргументы на самом деле изменяются и своей изменчивостью затушевывают и искажают интересующую нас зависимость.

Второй основной задачей измерения связи является:

-  определение степени искажающего влияния прочих факторов на интересующую нас зависимость или в определении силы, с которой данная зависимость проявляется среди многообразия нарушающих ее воздействий.

Первая задача измерения связи включает определение формы связи функции с определяющим аргументом и заключается в нахождении так называемой теоретической линии регрессии. Процесс нахождения  теоретической линии регрессии заключается в выборе и обосновании типа кривой, связывающей функцию и определяющий аргумент и расчете параметров ее уравнения.

Чаще всего для рассматриваемых целей используют кривые, выражающиеся многочленами целых положительных степеней

`y_x = a + bx

``  y_x = a + bx + cx² и т.д., где  y_x – ордината теоретической линии регрессии

Многочлен первой степени выражает равномерный рост или уменьшение функции, второй – степени – равнозамедленное или равноускоренное изменение y_x с одним экстремумом.

Выбор аналитического вида получаемой зависимости зависит от профессиональной подготовки исследователя. Наиболее часто (в 80% случаев из 100%) предполагают наличие линейной зависимости. После того как выбран и обоснован тип уравнения регрессии, необходимо определить параметры, от которых зависит это уравнение.

Допустим, характер расположения точек на корреляционном поле и интуиция подсказывает нам, что теоретическая линия регрессии является прямой линией, т.е. выражается уравнением

`у_х = a + bx, где  a  и  b  - неизвестные параметры.

Для нахождения неизвестных a  и  b в уравнении прямой линии воспользуемся методом наименьших квадратов (МНК).

S(y_i - `y_x)² = min                                  (2.33)

т.е. потребуем, чтобы сумма отклонений фактических ординат от ординат, вычисленных по уравнению прямой была наименьшей.

Заменим в (2.33) `y_x  через (a + bx) и обозначим левую часть формулы через f

f = S(y_i - a - bx)² ® min

Значения   a и b,  удовлетворяющие условию миниума функции найдутся из выражений

¶f/¶a = 0,       ¶f/¶b =0

Произведя соответствующие преобразования, получим

¶f/¶a = - 2å(y_i - a – bx_i) = 0 Þ åy_i = n×a + båx_i

¶f/¶b = - 2å(y_i - a – bx_i) x_i = 0 Þ åy_i x_i= aåx_i + båx_i² получаем систему т.н. нормальных уравнений

åy_i = n×a + båx_i

åy_i x_i= aåx_i + båx_i²                            (2.34)

Решая  систему (2.34), отыскиваем коэффициенты   a и  b.

Если отыскивается по методу МНК зависимость `y_x = a + bx + cx²,

То соответствующая система нормальных уравнений будет следующей

åy_i = a n + båx_i + сåx_i²

                                 åy_i x_i= aåx_i + båx_i² + сåx_i³                              (2.35)

   åy_i x_i²= aåx_i² + båx_i³ + сåx_i⁴

Следующей задачей (корреляционного) анализа является измерение тесноты связи. Поясним это на схематическом примере (рис.2.11).

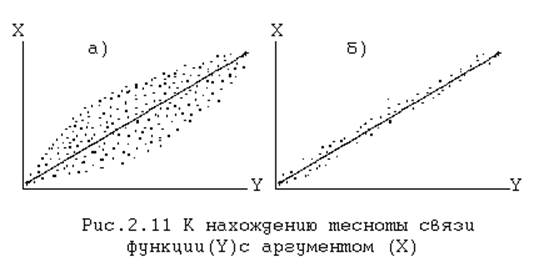Рассмотрим два корреляционных поля “а” и “б”. Пусть линии регрессии  Y по X  в обоих полях расположены одинаково. Однако, точки поля “б” значительно ближе примыкают к линии регрессии, чем точки поля “а”. Отклонения точек поля от линии регрессии объясняются, очевидно, влиянием прочих факторов. Если бы Y полностью определялся аргументом  X, то все точки поля находились бы на линии регрессии ; чем сильнее влияние всех прочих факторов, тем больше отклоняются от линии регрессии точки корреляционного поля.

Очевидно, что в случае “б” влияние аргумента X в меньшей степени осложняется действием прочих факторов, чем  в случае “а”, и зависимость между  Y и X является более тесной. Степень тесноты связи – весьма важное свойство, определяющее научное и практическое значение данной корреляционной зависимости.

Если теснота связи велика, то, зная аргумент, мы по уравнению регрессии достаточно точно предсказываем значение функции; воздействуя на аргумент, если он является причиной изменения функции, можно управлять функцией. Если теснота связи мала, то влияние аргумента  X  на функцию обнаруживается лишь в среднем по уравнению регрессии. В каждом же отдельном случае оно перекрывается действием побочных факторов.

Измерение тесноты корреляционной зависимости – вторая основная проблема теории корреляции. Рассмотрим пути ее решения.

Действие какого-либо фактора на функцию проявляется в изменчивости функции под влиянием изменчивости данного фактора. Поэтому показатель изменчивости функции – дисперсия – является одновременно показателем влияния на функцию изменчивости различных ее факторов.

Для того, чтобы выяснить степень влияния какого-либо одного из этих