













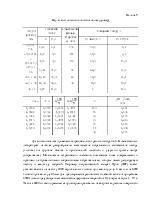







































суммарный выход класса, крупнее х, по плюсу, %; х — размер отверстий сита; b и n — параметры, зависящие от свойств материала и размерности х.
Соответствие опытных данных уравнению (7) можно проверить графически путем нанесения опытных точек на функциональную координатную систему. При двойном последовательном логарифмировании уравнение (7) приобретает вид
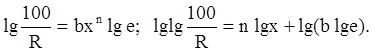
В координатах lglg![]() ,
lgх
уравнение Розина — Раммлера изображается
прямой линией с угловым коэффициентом n. Пример
построения такого графика (по данным табл. 8) показан на рис. 11, д.
,
lgх
уравнение Розина — Раммлера изображается
прямой линией с угловым коэффициентом n. Пример
построения такого графика (по данным табл. 8) показан на рис. 11, д.
На осях против соответствующих логарифмических величин приведены выхода классов и диаметры зерен материала.
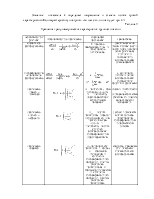
Параметры b и n уравнения (7) находят по двум известным точкам, решая систему уравнений:
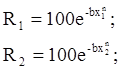
При совместном решении этих уравнений получим :
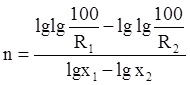 .
(8)
.
(8)
Зная n, определяем b:
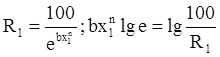 ;
;
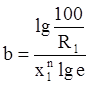 . (9)
. (9)
Уравнение Розина — Раммлера охватывает опытные точки в широком диапазоне крупностей, но оно не удовлетворяет одному конечному условию — нулевой выход классов достигается только при бесконечно большой крупности материала:
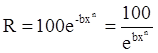 и R=0 при x=∞
и R=0 при x=∞
При использовании уравнения Розина — Раммлера приходится считаться с этим обстоятельством и принимать конечную крупность материала, соответствующую какому-то определенному значению выхода класса. Сливы классификаторов шаровых мельниц, работающих в замкнутом цикле, большей частью удовлетворяют уравнению Розина — Раммлера при n = 1 [1].
§ 7. Дифференциальные функции распределения по крупности
Дифференциальные функции распределения по крупности показывают число зерен или массовые выхода каждого класса крупности в данном материале. Материал, состоящий из смеси зерен разных размеров, разделенный на классы крупности, можно рассматривать как статистический коллектив. Размер зерен будет аргументом коллектива, а общее число зерен в пробе материала или ее общая масса составят числовой или массовый объем статистического коллектива. Число зерен в каждом классе или их массу называют численностью класса, частотой или абсолютной частостью, а частоты классов, отнесенные к объему коллектива, — относительными частостями классов.
Если в прямоугольных координатах по оси абсцисс отложить крупность классов и на соответствующих интервалах крупности построить прямоугольники, площади которых будут пропорциональны частоте класса, то получим гистограмму распределения зерен материала. Это равнозначно построению прямоугольников высотой, равной частости на единицу длины интервала, на интервале как основании прямоугольника. При уменьшающемся интервале ступенчатая линия, сверху ограничивающая прямоугольники, приближается к плавной кривой; в пределе она дает дифференциальную функцию распределения (рис. 11, е). Ординаты функции распределения γ(x) выражают частость на единицу длины бесконечно узкого интервала по оси абсцисс, а площадь под кривой определяет число объектов (число зерен, массовый выход их) в соответствующих промежутках.
Зерна, диаметры которых меньше хn и больше хn-1 образуют n-й класс — хn+хn-1 с интервалом крупности Δxn= хn – хn-1. Если число зерен в этом классе Nn, а масса их Wn, то относительная частость по числу зерен будет Nn/n и по массе Wn/W, где N — общее число зерен в пробе материала, а W — их общая масса.
Таким образом, для построения функции распределения по числу зерен следует по оси абсцисс на интервале xn – xn-1 построить прямоугольник высотой Nn/NΔxn, а затем — прямоугольники для всех других классов и соединить кривой точки на серединах верхних сторон прямоугольников. Относительное число зерен в бесконечно малом интервале dx
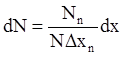
и в классе хп - хп-1
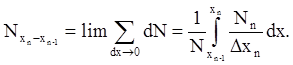
Аналогично имеем следующее выражение для массовых выходов зерен класса хп - хп-1:
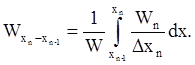
Последнее выражение соответствует уравнению (3) в следующей записи
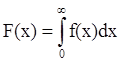
В этом уравнении пределы интегрирования определяют границы класса крупности, массовый выход которого определяется, а подынтегральная функция f(х) есть дифференциальное распределение по крупности, физическое и математическое толкование которой даётся в [27].
Кривые распределения дают более наглядное представление о гранулометрическом составе сыпучих материалов в сравнении с суммарными характеристиками крупности. В классах с наибольшим выходом кривая показывает максимум, а при отсутствии в материале зерен какого-либо размера — падает до нуля. Выхода класса на кривой распределения пропорциональны площадям, ограниченным кривой и двумя ординатами, проведенными на диаметрах, ограничивающих данный класс.
Дифференциальные функции распределения и суммарные характеристики крупности полностью характеризуют гранулометрический состав материала с точки зрения математической статистики. Возможен аналитический переход от одной кривой к другой, если известно уравнение какой-либо из них (см. формулу 3).
§ 8. Вычисление поверхности и числа зёрен по уравнениям суммарной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.