Другие предметы \ Объектно ориентированное програмирование

Вывод на экран изображение поверхности z=f(x,y) с удалением невидимых линий

Страницы работы

4 страницы (Word-файл)

Скачать файл

Фрагмент текста работы

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 3

Задание. Вывести на экран изображение поверхности z=f(x,y) с удалением невидимых линий.

Варианты заданий. Удаление невидимых линий осуществляется либо с использованием алгоритма плавающего горизонта (M1), либо с использованием метода художника (М2). Рассматривается либо центральная проекция (Р1), либо параллельная проекция (Р2). Поверхность задается одной из следующих формул:

Z1.	Z4.	Z7.
Z2.	Z5.	Z8.
Z3.	Z6.	Z9.

Получаем следующие варианты:

1) M1-P2-Z1	6) M1-P2-Z6	11) M2-P1-Z2	16) M2-P1-Z7	21) M2-P2-Z4
2) M1-P2-Z2	7) M1-P2-Z7	12) M2-P1-Z3	17) M2-P1-Z8	22) M2-P2-Z5
3) M1-P2-Z3	8) M1-P2-Z8	13) M2-P1-Z4	18) M2-P2-Z1	23) M2-P2-Z6
4) M1-P2-Z4	9) M1-P2-Z9	14) M2-P1-Z5	19) M2-P2-Z2	24) M2-P2-Z7
5) M1-P2-Z5	10) M2-P1-Z1	15) M2-P1-Z6	20) M2-P2-Z3	25) M2-P2-Z8

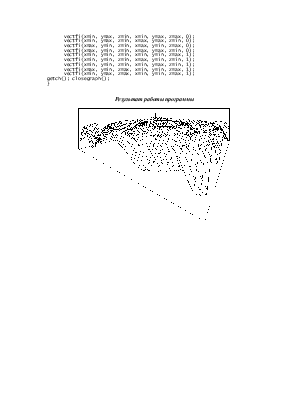
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ

Задание. Вывести на экран изображение поверхности z=sin(x²+y²) в центральной проекции, используя алгоритм плавающего горизонта для удаления невидимых линий.

Решение. Точки (x,y,z) вычерчиваемой части поверхности принадлежат некоторому прямоугольному параллелепипеду x_min£ x £ x_max, y_min£ y £ y_max, z_min£ z £ z_max. Точка наблюдения (x_V,y_V,z_V) удовлетворяет условиям x_V ³ x_max, y_V³ y_max, z_V³ z_max. Функции ex и ey переводят мировые координаты (x,y,z) в координаты проекции (x¢,y¢). Плоскость проекции имеет единичный вектор нормали u = (cosa, sina, 0) и находится на расстоянии d от точки (x_V, y_V,z_V) (см. рассмотренный ранее пример 3.3 на центральную проекцию). Координаты центральной проекции вычисляются по формулам:

x'=-d((x-x_V)(-sina)+(y-y_V)cosa)/((x-x_V)cosa+(y-y_V)sina);

y'=-d(z-z_V)/((x-x_V)cosa+(y-y_V)sina).

Вычислим наибольшие и наименьшие координаты отображаемого параллелепипеда

ex_min= ex(x_max,y_min,z_min), ex_max= ex(x_min, y_max, z_max),

ey_min= ey(x_max, y_max, z_min), ey_max= ey(x_min, y_min, z_max).

Прямоугольник ex_min£ ex £ ex_max, ey_min£ ey £ ey_max будет окном, отображаемым на область вывода, состоящую из точек, имеющих целые координаты

X = (ex-exmin)*getmaxx()/(exmax-exmin),

Y = (ey-eymin)*getmaxy()/(eymax-eymin).

Рассматривается прямоугольная сетка в плоскости Oxy с шагом hx = (xmax-xmin)/nx по x, и hy = (ymax -ymin )/ny - по y .

Каждому прямоугольнику