Анализ доходности и риска активов в портфеле. Эффективные портфели. Выбор оптимального портфеля

Анализ доходности и риска активов в портфеле. Эффективные портфели. Выбор оптимального портфеля.

Ожидаемая доходность портфеля, т.е. набора активов, п.с. взвешенную среднюю из показателей ожидаемой дох-ти отдельных А-в, входящих в данный портфель:

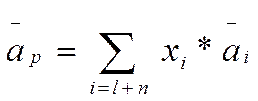
Где Xi-доля стоимости портфеля, инвестированная в i-й актив, аi – ожидаемая доходность i-го актива; i-порядковый номер актива, n- число активов в портфеле.

Риск портфеля в большинстве случаев меньше риска входящих в него активов. Для измерения риска портфеля необходимо вычислять среднее квадратическое отклонение его доходности.

Ковариация и коэф. Корреляции явл-ся основными понятиями, исп-ми для анализа риска портфеля.

Ковариация – мера, учитывающая дисперсию или разброс индивидуальных значений доходности акции либо других активов, и силу связи между изменением доходности данной акции и других акций. // ковариация м-у акциями А и Б показ-т, существует ли взаимосвязь м-у увеличением или уменьшением значения доходности этих акций , а кроме того, силу этой взаимосвязи. Ков-ия расчит-ся:

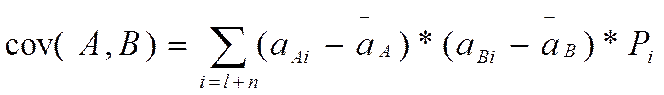
Где: Cov(А,В)-ковариация дох-ти акций А относительно дох-ти акций В; -ожидаемая доходность акций А; - ожидаемая дох-ть акций А при i-ом состоянии экономики; - ожидаемая дох-ть акций В; - ожидаемая дох-ть акций В при i-ом состоянии экономики; Рi-вероятность i-го состояния экономики, n-число возможных состояний экономики.

Корреляция – тенденция 2-х переменных к совместному изменению. Сила этой тенденции измеряется с пом. Коэф-та, кот. Лежит в пределах от +0,1 (что означает тождественное изменение переменных) до -0,1 (изменение значений 2-х переменных абсолютно противоположным образом). Если коэф-т =0, то связь отсутствует. Коэф-т корреляции рассчитывается:

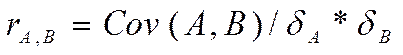, где: 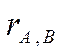- коэф-т коррел. М-у доходностью акций А и В;  - среднее квадратич. Отклонение доходности акций А;

Портфель, состоящий из нескольких активов.

Если распределения доходности отдельных ценных бумаг являются нормальными, то для определения риска портфеля, состоящего из нескольких активов, исп-ют след. Формулу: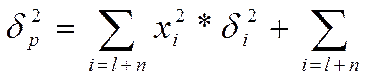 

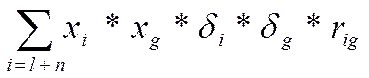
Где: 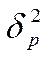-дисперсия доходности портфеля; 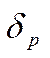- среднее квадратическое отклонение доходности портфеля; Xi и Xg- доли I-го и  g-го активов в портфеле;  и- средние квадратич. Отклонения доходности I-го и  g-го активов; n-число возможных состояний экономики;

Выбор эффективных портфелей, т.е. таких портфелей, кот. Обеспечивают max-ую ожидаемую доходность при определенном уровне риска или min-ый уровень риска для определенной ожидаемой доходности, является важной задачей фин. Менедж-та. При решении этой задачи учитывают статистические взаимосвязи доходности активов.

3 Графика: а)коэф. Коррел. =+0,1; б)коэф-т коррел. =0; в) воэф-т коррел-ии =-0,1.

Обычно менеджер располагает возможностями выбирать для формирования портфеля любые ценные бумаги, кот. Предлагаются на фин. Рынке. Из них он должен составить эффективное мн-во портфелей, для кот. Соотношение м-у риском и доходностью достигает максимума. (рис.б).

Портфель, состоящий из мн-ва активов. Если добавлять в портфель все большее кол-во новых акций, то риск портфеля будет быстро снижаться. Характеризовать риск портфеля, состоящий из мн-ва активов можно с пом. i-го коэф-та (йота-коэф-та), кот. Предст. Собой отношение среднего квадратич. Отклонения и ожид. Дох-ти. В простейшем случае йота-коэф. Исчисляется:

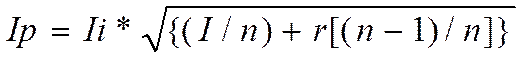
Где: Ip- йота-коэф. Доходности портфеля; Ii-взвешенное среднее йота-коэф. Активов, входящих в состав портфеля; n-число активов в портфеле; r-взвешенное среднее знасение коэф. Корреляции дох-ти активов, входящих в портфель. Используя эту формулу, можно установить, что с увеличением числа активов в портфеле риск быстро убывает.

Элементы общего риска акций- 2 составляющие риска: 1)несистематический, или диверсифицируемый риск, кот. Присущ отдельным акциям и может быть устранен путем формирования эффективного портфеля. 2) систематический или недиверсифицируемый или рыночный риск, кот. Присущ всему рынку акций и не может быть устранен за счет формирования портфеля.

Оптимальный портфель-тот единственный из эффективных портфелей, кот. Явл-ся наилучшим для конкретного инвестора. При выборе оптим. Портфеля решаются 2 задачи: 1) определение эффективного множества портфелей, 2) выбор из этого эффективного мн-ва единственного, наилучшего для конкретного инвестора.

Кривые безразличия «риск-доходность» п.с. характеристики конкретных инвесторов. Пример кривых безразличия конкретного инвестора в координатах «риск-доходность» приведены на рис. 2

Портфель, оптимальный с т.зр. инвестора, соответст. Точке касания кривой, характериз-ей эффективное мн-во портфелей