




















7 Нелинейные системы автоматического управления
Строго линейных систем не существует. Линейная система на самом деле является линейной моделью реальной автоматической системы. Но в некоторых реальных системах возникают явления, необъяснимые в рамках линейной теории: зависимость характера процессов от начальных условий и внешних воздействий, существование нелинейных колебаний и др. явления. Обычно в линейной системе бывает только одно нелинейное звено, реже 2 или 3.
7.1 Разновидности нелинейных звеньев
1. Звено с релейной статической характеристикой.
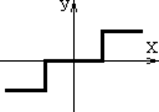
Рис. 7.1
В файле релейная характеристика приведены блоки relayc разной шириной зоны нечувствительности DeadBand. На выход выдается всегда либо +1, либо -1. меняя ширину зоны нечувствительности, пронаблюдайте за изменением формы выходного сигнала, снимаемого с релейного звена.
2 Звено со статической характеристикой кусочно-линейного типа (с зоной нечувствительности и ограничением)
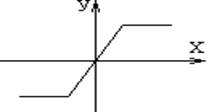 .
.
Рис. 7.2
Зона нечувствительности в Vissim реализуется блоком deadband. Ширина зоны нечувствительности находится во вкладке clearbandproperties. Изменяя этот параметр проследите, как меняется форма выходного сигнала вплоть до полного его исчезновения, когда ширина зоны нечувствительн6ости равна удвоенной амплитуде входного сигнала.
Ограничения. В Vissim реализуется блоком limit. В нем можно устанавливать уровни ограничения LimitProperties. Устанавливается нижняя граница (LowerBound) и верхняя граница (UpperBound). Изменяя уровни границ пронаблюдайте, как изменится форма выходного сигнала, когда на вход звена подано синусоидальное воздействие. Замените генератор синусоидального сигнала на генератор ступеньки (step). Как в этом случае влияет изменение уровня ограничения на форму выходного сигнала?
3. Звено с криволинейной статической характеристикой.
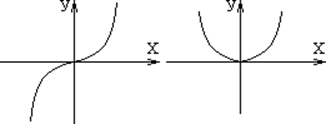
Рис. 7.3
4.Звено, дифференциальное уравнение которого нелинейно за счет входящих в него произведений переменных ,или их производных.
5.Звено, работа которого связана с выполнением логических операций.
Нелинейности делятся на сопутствующие (неизбежно присутствующие): это люфты (зазоры), трения в механических передачах, насыщения в усилителях, ограничения (мех. упоры, концевые выключатели) и преднамеренно вводимые для улучшения качественных показателей.
Специфическая особенность нелинейных систем – возникновение автоколебаний, которые существуют при отсутствии внешних воздействий (периодических) только за счет внутренних свойств систем и имеют определенную амплитуду и частоту.
В нелинейных системах не применим принцип суперпозиции. у(х1+х2) ≠ у(х1)+у(х2).
7.2 Метод гармонической линеаризации
Он применим для приближенного исследования процессов в замкнутых нелинейных системах, описываемых дифференциальным уравнением любого порядка.. Разомкнем систему и подадим воздействие x = Asinωt, тогда на выходе будет периодический, но в общем случае не синусоидальный сигнал
у = F(A sinωt). (1)
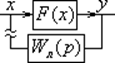
Рис.7.4
При подаче гармонического сигнала на вход линейной системы на выходе всегда получается гармонический сигнал той же частоты, отличающийся только амплитудой и фазой. Разложим (1) в ряд Фурье: у = Со+D1 sinωt+C1cosωt+D2sin2ωt+ C2cos2ωt+….
Для нелинейных характеристик симметричных по отношению к началу координат Со =0. Нелинейная часть системы обычно плохо пропускает высокие частоты, поэтому ограничимся только первой гармоникой: : у =D1 sinωt+C1cosωt .
На основании x = Asinωt имеем sinωt=х/А ,а
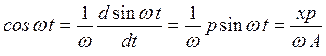 .
.
Поэтому
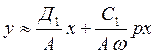
Получили линейное уравнение, но его коэффициенты зависят от амплитуды и частоты.
7.3 Коррекция нелинейных систем
Псевдолинейные корректирующие устройства.
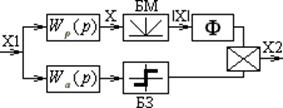
Рис.7.5
БМ – блок модуля, БЗ – блок знака, Ф – фильтр.
В БМ используется выпрямитель. Фильтр выделяет постоянную составляющую. Нижний канал определяет фазу. БЗ исключает информацию об амплитуде. Сигналы на выходе перемножаются.
7.4 Фазовые траектории
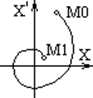
Рис.7.6
Состояние системы n-го порядка в любой момент времени полностью определяется значениями n-независимых переменных (координат). Если построить n-мерное пространство, по осям которого отложены координаты системы, то они определят некоторую точку, называемую изображающей, а пространство называется фазовым (пространство состояний). Если с течением времени происходит изменение координат, то изображающие точки перемещаются, описывая кривую, которая называется фазовой траекторией. Движение точки по фазовой траектории представляет собой геометрическую интерпретацию процессов в системе. Чаще всего метод фазовых траекторий применяется для исследования
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.