Емкостный метод измерения и контроля технологических параметров. Индуктивные методы и средства неразрушающего контроля параметров технологических процессов

Коэффициенты регрессии  являются оценкой истинных коэффициентов регрессии  в теоретической линейной зависимости вида:

                                                      (1.18)

6.  Определение коэффициентов  регрессии производится по формулам:

                                                   (1.19)

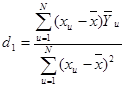                                                     (1.20)

Расчеты необходимых сумм сводим в таблицу 1.3.

Определяем значения  Подставив их в выражение (1.16) получим искомое уравнение регрессии.

Таблица 1.3 - Результаты расчетов

U
1	0
2	5
3	10
4	15
5	20
6	25
	75

7.  Определение адекватности полученного уравнения:

Расчетное значение критерия Фишера:

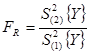                                                               (1.21)

где - средняя дисперсия или дисперсия воспроизводимости

 - дисперсия, характеризующая рассеивание средних экспериментальных значений   относительно , т.е. относительно прямой линии.

Эта дисперсия характеризует точность аппроксимации зависимости  прямой линией  и определяется по формуле:

                                                             (1.22)

Число степеней свободы этой дисперсии . Подставляя значение дисперсии в формулу (1.21) получаем:

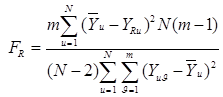                                   (1.23)

Расчет сумм для формулы (1.22) сведем в таблицу 1.4. Расчетное значение F_R сравнивают с табличным значением критерия Фишера F_T, которое определяют при доверительной вероятности P_Д = 0,95 и числе  степеней  свободы  дисперсий

 и . Если F_R < F_T, то гипотеза об адекватности линейного уравнения (1.16) опытным данным не отвергается.

Таблица 1.4 - Результаты расчетов

Определение значимости коэффициентов регрессии и их доверительных интервалов:

Для оценки значимости используется критерий Стьюдента, расчетное выражение которого определяют по формуле:

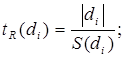                                                                      (1.24)

где  оценка среднего квадратического отклонения коэффициента регресии  d_i.

Оценку дисперсий коэффициентов d₀ и d₁ в уравнении (1.16) определяют по формулам:

                                                         (1.25)

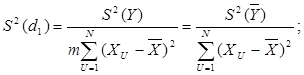                                  (1.26)

                              (1.27)

Число степеней свободы этой дисперсии определяется выражением:

                                                                      (1.28)

Таким образом, методика расчета сводится к следующему:

-    по формуле (1.27) определяется

-    по формулам (1.25) и (1.26) определяются дисперсии коэффициентов регрессии

-    расчетное значение критерия Стьюдента определяется по формуле (1.24).

По таблице 7 приложения определяем табличное значение критерия Стьюдента для Р_Д  = 0,95 и числа степеней свободы, определяемого по формуле (1.28). Если t_R(d₀) > t_T и t_R(d₁) > t_T , то полученные коэффициенты значимы и следовательно, связь между Y и X значима.

9.  Определение доверительных интервалов средних значений выходного параметра при фиксированном значении фактора:

Чтобы убедиться, как сильно могут уклоняться расчетные значения выходного параметра Y_RU от истинного его значения при каждом уровне фактора X_U, определяют доверительные ошибки расчетного значения выходного параметра и доверительные интервалы истинного и среднего значения выходного параметра по формулам:

                                                  (1.29)

где                                    (1.30)

Расчетные значения  для каждого U – го уровня фактора свести в таблицу 1.5. Определяем табличное значение (табл.7 приложения) критерия Стьюдента и подстановкой его в формулу (1.29) определяем  для каждого уровня фактора, что заносим в таблицу 1.5, а также находим  и . Зная ошибки расчетной величины найти доверительные интервалы для средних значений выходного параметра, используя следующие неравенства:

           (1.31)

Результаты расчета заносим в таблицу 1.5. По данным таблицы 1.5 построить расчетную модель уравнения регрессии и ее доверительные интервалы в виде функции  и . Сделать вывод по результатам проделанной работы.

Таблица 1.5 - Результаты расчетов

Требования к отчету о лабораторной работе

Отчет должен включать следующие структурные элементы:

- титульный лист, выполненный в соответствии с формой А.5 образовательного стандарта СТП12570-2006;

- цель работы, изложенную в методических указаниях;

- основную часть работы, т.е. построение номинальной статистической характеристики ПИП и ее регрессионной модели с доверительными интервалами по данным проведенного эксперимента;

- выводы, которые должны отражать соответствие расчетной модели уравнения регрессии экспериментально снятой номинальной статической характеристики;

- список использованной литературы.

Правила техники безопасности при выполнении работы:

- к лабораторным работам допускаются студенты, прошедшие инструктаж по технике безопасности, что подтверждается личной подписью в журнале инструктажа;

- перед началом работы необходимо убедиться в наличии заземления у измерительных приборов и в отсутствии видимых повреждений;

- в процессе работы запрещается проникать внутрь приборов, касаться разъемов соединительных кабелей;

- при обнаружении искрения или при появлении запаха гари следует немедленно выключить аппаратуру и сообщить об этом преподавателю;

- при несчастном случае (поражении электротоком) необходимо обесточить пострадавшего, вызвать скорую помощь и приступить к оказанию доврачебной помощи;

- при пожаре необходимо обесточить помещение лаборатории, вызвать пожарную охрану и приступить к тушению пожара огнетушителем.

Контрольные вопросы:

1.  Принципы действия емкостного ПИП.

2.  Функцией каких величин является емкость ПИП?

3.  Основные типы емкостных преобразователей, их достоинства и недостатки.

4.  Назовите пути улучшения метрологических характеристик емкостных