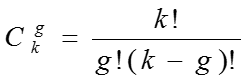Полный факторный эксперимент типа Свойства ПФЭ типа ПФЭ и математическая модель
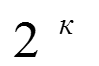
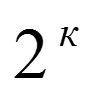
-
ПФЭ типа -Эксперимент в котором реализуются все возможные сочетания уровней факторов, если каждый из факторов имеет только два уровня
-
Общее число опытов
-
K-число факторов, m- число уровней
-
В случаи эксперимента общее число опытов составит
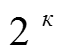
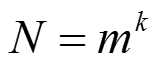
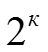
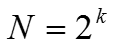
-
Результаты эксперимента представляют в виде таблиц.
-
Строки- различные опыты, Столбцы- значения которые принимают факторы. Такие таблицы- матрицы планирования.
-
Уровни, которые принимают факторы обозначаются как нижний - 1, верхний +1 уровни.
-
Каждому фактору присваивается буква a, b, c, d
-
Если фактор находится на верхнем уровне, то буква записывается в обозначение, если оба на нижнем уровне, то ставится (1)
-
Способы заполнения матриц планирования
-
1. Метод перевода: При добавлении нового фактора каждая комбинация уровней исходного плана повторяется дважды, для 1 комбинации исходного плана значение верхнего нового фактора соответствует верхнему уровню, для второй- нижнему.
-
2. Метод перемножения: Для 1ой исходной комбинации производится построчное перемножение столбцов, результат записывается в столбец нового фактора, для 2ой построчное перемножение столбцов, результат с обратным знаком.
-
3. Метод чередования знаков: В 1ом столбце знаки чередуются (+,-,+,-,), во 2ом знаки попарно (+,+,-,-), в 3ем по четыре.
-
Свойства матриц типа
-
1. Симметричность относительно центра эксперимента: алгебраическая сумма элементов вектор-столбца каждого фактора = 0;
-
2. Условия нормировки: сумма квадратов элементов каждого столбца = числу опытов;
-
3. Свойство ортогональности: сумма почленных произведений любых двух вектор-столбцов матрицы = 0;
-
4. Свойство ротатабельности: точки в матрице планирования подбираются таким образом, чтобы точность предсказаний значений параметра оптимизации одинаково на равных расстояниях от центра эксперимента и не зависит от направления в котором проводится планирование.
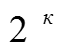
-
ПФЭ и математическая модель
-
Вид математической модели
-
Поиск коэффициентов проводится с помощью регрессионного анализа или с помощью матриц планирования по формуле
-
или
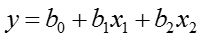
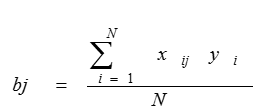
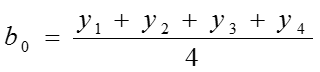
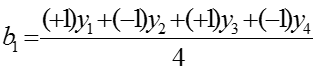
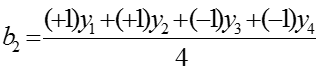
-
Если учитывать влияние взаимодействия факторов, то модель эксперимента
-
При планировании эксперимента условия опыта определяют по столбцам , а и используют только для расчёта эксперимента
-
Взаимодействие факторов - эффект первого порядка
-
Число всех эффектов некоторого порядка определяют по формуле
-
k-число факторов
-
g-число элементов во взаимодействии
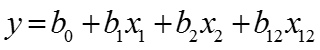
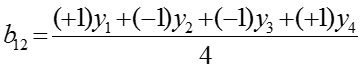
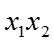
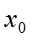
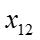
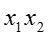
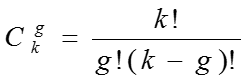
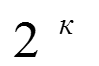
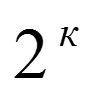
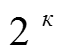
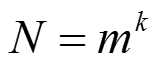
![]()
![]()
![]()
![]()
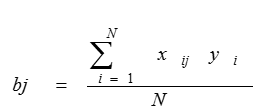
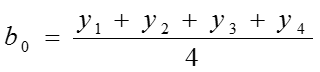
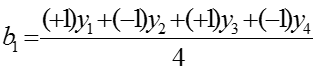
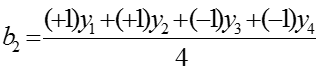
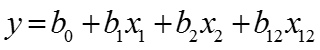
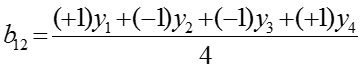
![]()
![]()
![]()
![]()