Полный факторный эксперимент типа (ПФЭ). Метод перевода (метод зеркального отражения). Метод перемножения

ТЕМА: Полный факторный эксперимент типа  (ПФЭ-)

ПФЭ – эксперимент, в котором реализуются все возможные сочетания уровней факторов, если каждый из факторов имеет только два уровня, то такой эксперимент называется типа .

Зная число факторов можно вычислить общее число опытов для полного факторного эксперимента. N=, где К–число факторов, m - число уровней.

В случае эксперимента типа , общее число испытаний составит N=. Наиболее удобно результаты эксперимента представлять в виде таблице, каждая строка которой соответствует различным опытам, а столбцы – значениям, которые принимают факторы или параметр оптимизации. Эти таблицы называются матрицами планирования или планами эксперимента:

Буквенное обозначение: аb=;  b=;  a=;  (1)= .

В случае эксперимента типа , уровни, которые принимают факторы обозначаются как нижний -1 и верхний +1 уровни.

Каждый столбец матрицы является вектор-столбец, а строка – вектор-строка.

Часто при написании матрицы планирования используется буквенное обозначение. Каждому фактору присваивается буква латинского алфавита: a, b, c, d. Пропуск букв не допускается. Если фактор находится на верхнем уровне, т.е. =+1, то соответствующая буква записывается в обозначение, если фактор находится на нижнем уровне, то соответствующая буква опускается, если оба на -1, то ставится (1).

Наиболее проблематичным  является заполнение вектор-столбцов факторов таким образом, чтобы учесть все возможные сочетания уровней факторов, не продублировав и не пропустив какое-либо сочетание. Существует несколько способов заполнения матриц планирования. Два из них состоят в переходе от матрицы более низкой размерности к матрице более высокой размерности.

Рассмотрим на примере перехода от  к :

1.  Метод перевода (метод зеркального отражения)

При добавлении нового фактора, каждая  комбинация уровней исходного плана повторяет дважды, при этом для первой комбинации исходного плана, значение верхнего нового фактора соответствует верхнему уровню, для второй – нижнему.

)                                                             )

2.  Метод перемножения

Для первой исходной комбинации выполняем построчное перемножение столбцов, а результат записываем в столбец нового фактора. Для второй комбинации – построчное перемножение столбцов, а в столбец нового фактора записываем результат с обратным знаком.

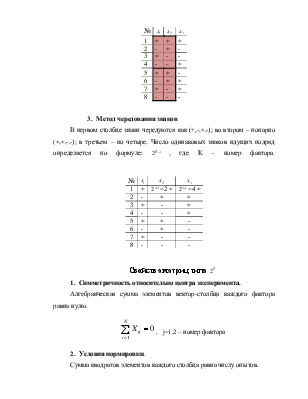
3.  Метод чередования знаков

В первом столбце знаки чередуются как (+,-,+,-); во втором – попарно (+,+,-,-); в третьем – по четыре. Число одинаковых знаков идущих подряд определяется по формуле: , где К – номер фактора.

Свойства матриц типа

1.  Симметричность относительно центра эксперимента. 

Алгебраическая сумма элементов вектор-столбца каждого фактора равна нулю.

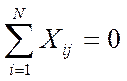,   j=1,2 – номер фактора

2.  Условия нормировки.

Сумма квадратов элементов каждого столбца равна числу опытов.

3.  Свойство ортогональности.

Сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю.

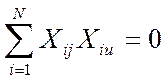
u,j=1,2 – номер фактора; u≠j

4.  Свойство ротатабельности

Точки в матрице планирования подбираются таким образом, чтобы точность предсказания значения параметра оптимизации было одинаково на равных расстояниях от центра эксперимента и не зависело от направления, в котором проводится планирование.

ТЕМА:  ПФЭ- и математическая модель

Для эксперимента типа  математическая модель эксперимента, если не будет учитываться влияние взаимодействия факторов, будет иметь вид:

Поиск коэффициентов модели можно производить с помощью регрессионного анализа или с помощью матриц планирования. Процедура поиска коэффициентов с помощью матрицы планирования производится по формуле:

(*); 

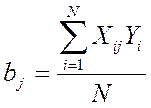Пример:

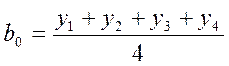
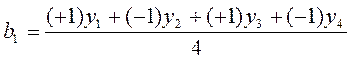
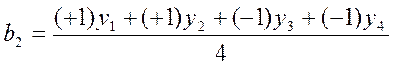
Формула (*) может использоваться и для поиска коэффициентов , если для этого ввести служебный столбец  , значения в котором равны +1, то:

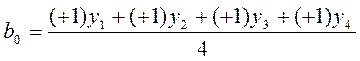
Если учитывать влияние взаимодействия факторов, модель эксперимента примет вид:

В этом случае для расчета коэффициента  можно использовать (*), введя в матрице служебный столбец , тогда:

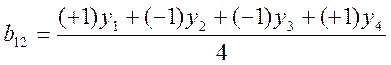
При планировании эксперимента условие опыта определяют только по столбцам , а и используют для расчета эксперимента. Взаимодействие факторов называют эффектом взаимодействия факторов.

Эффекты типа  называют парными или эффектами первого порядка.  Эффекты типа  -  тройными или эффектами второго порядка.

Максимальный порядок эффекта взаимодействия, возможный в ПЭФ, будет на единицу меньше числа факторов, участвующих в этом эксперименте.

Полное число всех возможных эффектов взаимодействия, линейных эффектов (действия самих эффектов), а также , равное числу опытов ПЭФ. Число всех эффектов некоторого порядка  можно определить по формуле:

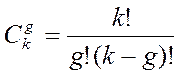
К – число факторов, g – число элементов во взаимодействии.