









Контрольная работа
2 семестр, ОЗО
Вариант 0
Задание№1. Найти производные первого порядка данных функций, используя правила вычисления производных.
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
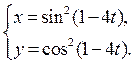
Задание № 2. Вычислить приближенное значение функции, применяя
дифференциал функции.![]()
Задание № 3. Решить задачу на экстремум.
Пункт А находится на расстоянии 60 км от железной дороги. Расстояние по железной дороге от пункта А до ближайшего к пункту В точки С составляет 285 км. На каком расстоянии от точки С надо построить станцию, от которой проложат шоссе к пункту В, чтобы затрачивать наименьшее время на продвижение между пунктами А и В, если скорость движения по железной дороге равна 52 км/ч, а скорость движения по шоссе – 20 км/ч.
(ответ:25 км/ч)
Задание № 4. Вычислить: а) неопределенный интеграл; б) неопределенный интеграл; в)неопределенный интеграл; г) определенный интеграл.
Задание № 5. Решить задачу.
Вычислить объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной параболой у = х2 + 1 и прямыми х=3, х=-3
Задание
№ 6.Даны два комплексных
числа:![]() и
и![]() .
Найти:
.
Найти:
а)
z1+z2;б)
z1-z2;
в)z1z2;
г) z1/z2;
д) представить в тригонометрической форме Z
=![]() i
i
Контрольная работа
2 семестр, ОЗО
Вариант 1
Задание№1. Найти производные первого порядка данных функций, используя правила вычисления производных.
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
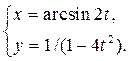
Задание
№ 2. Вычислить приближенное
значение функции, применяя дифференциал функции.![]()
Задание № 3. Решить задачу на экстремум.
Полотняный
шатер объемом Vимеет форму прямого
конуса. Каково должно быть отношение высоты конуса к радиусу его основания,
чтобы на шатер пошло наименьшее количество полотна? (ответ:![]() )
)
Задание № 4. Вычислить: а) неопределенный интеграл; б) неопределенный интеграл; в)неопределенный интеграл; г) определенный интеграл.
Задание № 5. Решить задачу.
Найти площадь фигуры, ограниченной линиями: у2 = 9х, у = 3х
Задание
№ 6.Даны два комплексных
числа:![]() и
и![]() .
Найти:
.
Найти:
а)
z1+z2;б)
z1-z2;
в)z1z2;
г) z1/z2;
д) представить в тригонометрической форме Z=![]() i
i
Контрольная работа
2 семестр, ОЗО
Вариант 2
Задание№1. Найти производные первого порядка данных функций, используя правила вычисления производных.
1) ![]() 2)
2)
![]()
3) 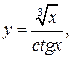 4)
4)
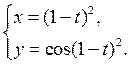
Задание № 2. Вычислить приближенное значение функции, применяя
дифференциал функции.![]()
Задание № 3. Решить задачу на экстремум.
Найти соотношение между радиусомR ивысотой H цилиндра, имеющего при данном объеме V наименьшую полную поверхность. (ответ:H = 2R)
Задание № 4. Вычислить: а) неопределенный интеграл; б) неопределенный интеграл; в)неопределенный интеграл; г) определенный интеграл.
Задание № 5. Решить задачу.
Вычислить
площадь поверхности, образованного вращением вокруг оси Ох дуги кривой у
= ![]() и
прямыми х=1, х=0
и
прямыми х=1, х=0
Задание
№ 6.Даны два комплексных
числа![]() и
и![]() .
Найти:
.
Найти:
а)
z1+z2;б)
z1-z2;
в)z1z2;
г) z1/z2;
д) представить в тригонометрической форме Z=![]()
Контрольная работа
2 семестр, ОЗО
Вариант 3
Задание№1. Найти производные первого порядка данных функций, используя правила вычисления производных.
1) ![]() 2)
2)
![]()
3) ![]() 4)
4)
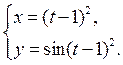
Задание
№ 2. Вычислить приближенное
значение функции, применяя дифференциал функции.![]()
Задание № 3. Решить задачу на экстремум.
Проволокой, длина которой lм, необходимо огородить клумбу, имеющую форму кругового сектора. Каким должен быть радиус круга, чтобы площадь клумбы была наибольшей? (ответ:l/4м)
Задание № 4. Вычислить: а) неопределенный интеграл; б) неопределенный интеграл; в)неопределенный интеграл; г) определенный интеграл.
Задание № 5. Решить задачу.
Найти площадь фигуры, ограниченной линиями: у= 4х –х2, у = х
Задание № 6.Даны два комплексных числаz1=1+3iиz2=-2+i.Найти:
а) z1+z2;б) z1-z2; в)z1z2; г) z1/z2; д) представить в тригонометрической форме z =-2-2i
Контрольная работа
2 семестр, ОЗО
Вариант 4
Задание№1. Найти производные первого порядка данных функций, используя правила вычисления производных.
1) ![]() 2)
2) ![]()
3) 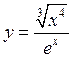 4)
4)
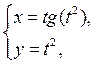
Задание № 2. Вычислить приближенное значение функции, применяя дифференциал функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.