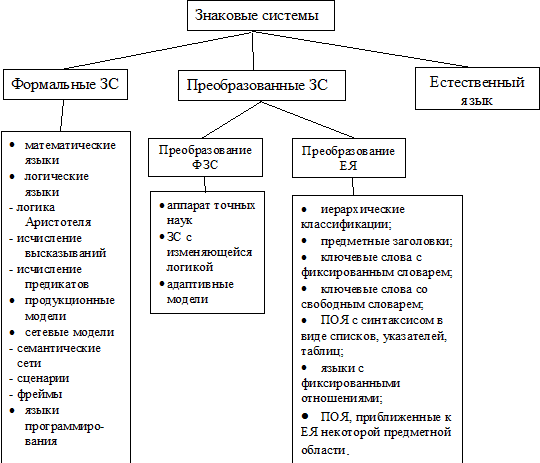
Логика Аристотеля. Исчисление высказываний. Исчисление предикатов. Правила вывода ИП

       

Логика Аристотеля

Базовые объекты: сущность S, классы сущностей, кванторы ", , знак выводимости |—

Базовые высказывания:

1. А: Всякий S есть Р;  2. Е: Всякий S не есть Р; 3. I: Некоторый S есть Р; 4. О Некоторый S не есть Р; 5. S есть Р; 6. S не есть Р; 7. a есть Р; 8. a не есть Р

Выводы ранга 0 – законы силлогистики: тождества, противоречия, исключенного третьего.

Выводы ранга 1 специального названия не имеют.

Выводы ранга 2 – силлогизмы Аристотеля. 256 модусов, из них 24 правильных.

Примеры.

·  Модус первой фигуры ААА имеет вид:

Всякий М есть Р                                 Всякая птица имеет перья.

Всякий S есть М                                Всякий дятел — птица.

---------------------                                ----------------------------------Всякий S есть Р                                  Всякий дятел имеет перья.

·  Модус первой фигуры EJO:

Всякий М не есть Р                                          Всякий дятел красиво не поет.

Некоторые S есть М                                         Некоторые птицы - дятлы.

-----------------------------      --------------------------------------Некоторые S не есть Р                      Некоторые птицы красиво не поют.

·  Модус четвертой фигуры IAO:

Некоторые Р есть М.                                        Некоторые люди - негры.

Всякий М есть S.                                Всякий негр - темнокожий

------------------------------                   ---------------------------------Некоторые S не есть Р.                     Некоторые темнокожие - не люди.

Исчисление высказываний

Алфавит ИВ:

·  переменные высказываний (пропозициональные буквы) А, В, С…;

·  знаки логических связок {Ù или & – «и», Ú– «или», ® – «если…то…», Ø или черта над формулой – «не»};

·  скобки (, ).

Формулы:

·  переменное высказывание есть формула;

·  если  Y и W – формулы, то (YÚW),(Y&W), (Y®W) и ØY – формулы;

·  других формул нет.

Аксиомы. А®(В®А);

(А®(В®С) ®(А®В) ® (А®С);

(ØА®ØВ) ®((ØА® В) ®А).

Правила вывода.

·  Правило подстановки: если Y – выводимая формула, содержащая букву А (обозначим этот факт Y(А)), то выводима формула Y(W), которая получается из Y заменой всех вхождений А на произвольную формулу, т.е.

W; Y(А)

-----------;

Y(W)

·  Правило заключения (modus ponens): если Y и Y®W – выводимые формулы, то W выводима, т.е.

Y; Y®W

------------.

W

Исчисление предикатов

Алфавит ИП:

·  предметные переменные x₁, x₂,..., x_n, принимающие значения из некоторой предметной области;

·  предметные константы a₁, a₂ , ... , a_m;

·  предикатные буквы (константы) P₁ , P₂ , ... , P_K;

·  функциональные буквы (константы)  f₁ , f₂ ,..., f_q;

·  знаки логических связок. Ú , & , ┐, → ;

·  кванторы ", ;

·  скобки ( , ).

Формулы ИП. Понятие формулы ИП определяется в два этапа.

Формулы А и B ИП называются равносильными (эквивалентными), если общезначима формула (А → B) & (B → А).

Этот факт отмечается как A = B или B = A. Основные равносильные формулы ИП представлены ниже.

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 

Соответствие между высказываниями силлогистики и формулами ИП.

A – "Всякое s есть р"                        .

E – "Всякое s не есть р"                    .

I – "Некоторые s есть р"                   .

O – "Некоторые s не есть р"            .

Аксиомы ИП аксиомы исчисления высказываний + предикатные аксиомы: "xF(x) →F(y); F(y) →xF(x).

Правила вывода ИП

·  правило заключения (modus ponens): если Y и Y®W – выводимые формулы, то W выводима, т.е.

Y; Y®W

-----------W

– то же, что и в исчислении высказываний;

·  правило обобщения ("-введения):

F→G(x)

--------------,

F→"xG(x)

где G(x) содержит свободные вхождения х, а F их не содержит.

·  правило -ввведения:

G(x) ® F

-----------------,

 xG(x) ® F

где G(x) содержит свободные вхождения х, а F их не содержит.

Сколемизация: замена  на выражение Ø"АØ.

Иинтерпретация I – четверка (D, I_С , I_P , I_υ ). Пример. Формула  yQ(y)→Q(x) в интерпретации: D – множество натуральных чисел; Q – предикат "Быть простым"; x=4. принимает  значение "Ложь".

А вы, друзья, как ни садитесь, все ж в музыканты не годитесь! "x¬ P(x,y).

Деталь № 1244 обрабатывается на станке  (arI) Ù (adb),

Между роботом и складом находится яма, слева от которой расположен экскаватор Р1(а, b) Ù Р2(а, b, с).

Вывод на знаниях  – показать общезначимость A₁ & A₂ & ... & A_n®B или невыполнимость¬ (A₁ &A₂ & ... & A_n ® B), 

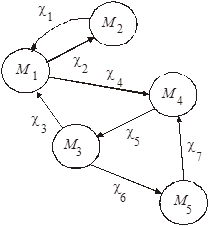
Сетевые модели  H=<I, C₁, …, C_n, Г>

Семантические сети

  

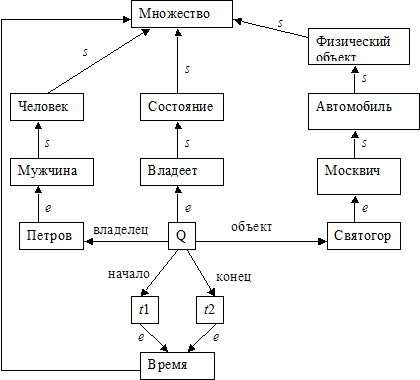
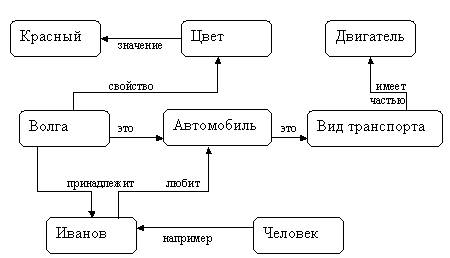
1:                                 ®C(a)                   (буква "истина" в условии опускается)

2:                          P(y) ®L(a,y)

3:  C(x)&H(y)&L(x,y) ®                        (буква "ложь" в заключении опускается)

4:                                 ®P(b)

5:                                 ®H(b)

                

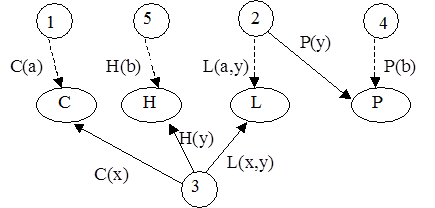
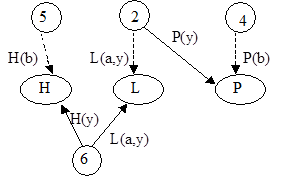
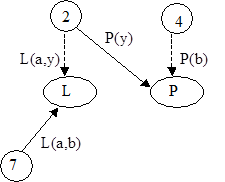
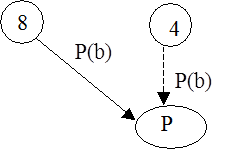
Сценарий

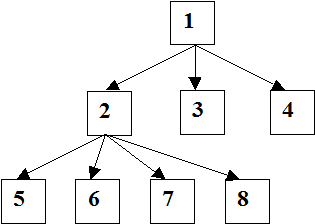
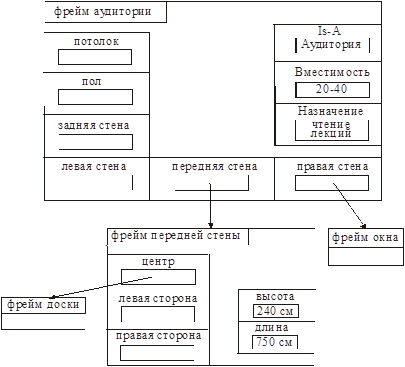
Фрейм

 

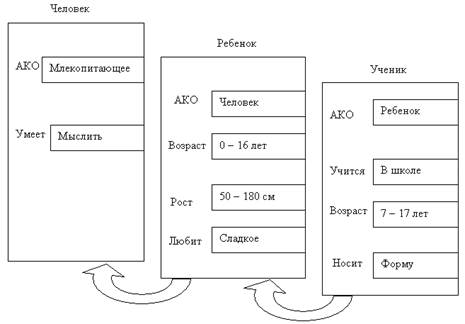
Продукционные модели  (i); Q; P; AÞВ; N.

    

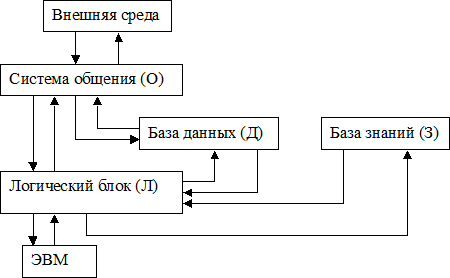
AÞВ	О	Д	З	Л
О		+		+
Д	+	+	+	+
З	+		+	+
Л	+		+	+