






САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРССТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
Отчет по лабораторной работе № 3
«Изучение методов помехоустойчивого кодирования»
Выполнили:
Санкт-Петербург
2011 год
Цель работы.
Изучение методов помехоустойчивого кодирования. Исследование характеристик помехоустойчивых кодов.
Вариант № 10.
Порождающая матрица линейного блокового кода.
%0. Открываю порождающую матрицу
G = importdata(' lab3_10.mat');
G =
1 0 0 1 0 1 1 1 0 0
0 0 1 0 1 0 1 0 1 0
0 0 0 1 1 1 1 1 1 0
0 0 0 0 0 1 1 0 1 0
0 0 0 0 1 1 1 1 0 1
0 1 1 1 1 1 1 1 0 1
%Количество бит в слове 6
k = size(G,1);
%Количество слов в предложении 10
n = size(G,2);
%Длина сообщения в битах 1020
MesLength = 1020;
%Число Закодированных Бит 1700
InCodedNums = MessLength/k*n
Теоретическая часть
Порождающей матрицей
линейного ![]() -кода называется матрица размера
-кода называется матрица размера ![]() ,
строки которой – его базисные векторы.
,
строки которой – его базисные векторы.
Базисом линейного пространства называется наибольшее возможное множество линейно независимых векторов пространства.
Число базисных векторов называется размерностью пространства.
кодовые слова –
линейные комбинации базисных векторов, т.е. строк матрицы ![]() .
.
Вычисляемые данные.
|
1 |
Определить минимальное расстояние линейного блокового кода |
|
CodeMinDist |
|
|
Теория |
Минимальным расстоянием кода
Для линейного кода эта формула может быть упрощена:
|
|
Исполняемый код |
%1. Минимальное расстояние линейного блокового кода rasst = []; for i = 1:k for l = 1:k if (l==i) continue end temps = 0; for j = 1:n if (G(i,j)~=G(l,j)) temps = temps+1; end end rasst = [rasst temps]; end end CodeMinDist = min(rasst); |
|
Значение |
3 |
|
2 |
Определить количество ошибок, исправляемое данным кодом |
|
FixError |
|
|
Формула |
код с минимальным расстоянием |
|
Исполняемый код |
%2.Колличество ошибок исправляемое данным кодом FixError = (codeMinimalDistance-1)/2; |
Значение |
1 |
|
3 |
Сгенерировать двоичное сообщение большой длины с равновероятными значениями нуля и единицы. |
|
BinaryMess |
|
|
Теория |
Линейным двоичным кодом |
|
Исполняемый код |
%3. Генерируем сообщение из двоичных значений BinaryMess=round(rand(1, MessLength)); |
4 |
Сгенерировать список кодовых слов |
|
CodeWords |
|
|
Теория |
кодовые слова – линейные комбинации базисных векторов,
т.е. строк матрицы кодовое слово вычисляется по формуле вектор из |
|
Исполняемый код |
%4 %генерация кодовых слов Combinations = GetCodeWords(wordLength); CodeWords = zeros(length(Combinations(:,1)), n); for i=1:length(Combinations(:,1)) CodeWords(i, 1:n) = (Combinations(i, 1:k))*G; end; CodeWords=mod(CodeWords,2); |
|
function GetCodeWords |
function res = GetCodeWords (n) max_number = 2^n-1; res = []; qw = zeros(1, n); for (i=1:1:max_number) number =i; temp=[]; while number>0 dev = mod(number,2); if (dev==1) s = (number - 1)/2; temp=[1 temp]; number = s; else s=number/2; temp = [0 temp]; number = s; end; end; disp(qw); if(length(temp)<n) temp =cat(2,zeros(1, n-length(temp)),temp); end; disp(temp); qw = vertcat(qw, temp); end; res = qw; |
5 |
Разбить передаваемую последовательность на блоки и произвести кодирование. |
|
CodeMess |
|
|
Исполняемый код |
%5. Kодирование сообщений CodeMess = []; for i = 1 : k : MessLength temp = Messages(i : i + k - 1); CodeMess = [CodeMess temp * G]; end; CodeMess = mod(CodeMess, 2); |
6 |
Сгенерировать вектор шума с вероятностью ошибки p. |
|
Исполняемый код |
P_error = 1/num_exp * count; P_ERR(1, count) = P_error; %генерация ошибок Errors = rand(1, InCodedNums); Errors = RoundX(Errors, P_error); |
7 |
Внести ошибки в закодированное передаваемое сообщение |
|
Исполняемый код |
%добавление ошибок Error_code = CodeMess + Errors; Error_code = mod(Error_code, 2); |
8 |
Произвести декодирование зашумленного сообщения. |
|
Исполняемый код |
%поиск близлежащих слов Decode = []; for i=1:n:InCodedNums cod = Error_code(i:i+n-1); min_dist=n; num=1; for j=1:length(CodeWords(:,1)) dist=0; for q=1:n if (cod(q) ~= CodeWords(j,q)) dist = dist +1; end; end; if (dist<=min_dist) min_dist=dist; num=j; end; end; Decode = [Decode Combinations(num, 1:k)]; end; |
9 |
Вычислить вероятность ошибки на бит. |
|
Исполняемый код |
%оценка ошибки по битам bit_errors = 0; for i=1:MessLength if (BinaryMess(i) ~= Decode (i)) bit_errors = bit_errors +1; end; end; %fprintf('Оценка вероятности ошибок по битам : %4.2f.\n', bit_errors/messageLength); P_ERR(2, count) = bit_errors/MessLength; |
10 |
Вычислить вероятность ошибки на байт. |
|
Исполняемый код |
%оценка ошибки по байтам bite_errors = 0; for q=1:MessLength/k for w=1:k if(Decode((q-1)*6 +w) ~= BinaryMess ((q-1)*6 +w)) bite_errors = bite_errors +1; break; end; end; end; %fprintf('Оценка вероятности ошибок по байтам : %4.2f.\n', bite_errors/messageLength*wordLength); P_ERR(3, count) = bite_errors/MessLength*k; |
11 |
Вычислить вероятность ошибки на байт. |
|
Исполняемый код |
P_ERR(4, count) = 0; for i=1:1:((CodeMinDist-1)/2+1) P_ERR(4, count) = P_ERR(4, count) + (prod(1:n)/prod(1:i-1)/prod(1:n-i+1)) * P_error^(i-1) * (1-P_error)^(n-i+1); end; %fprintf('Оценка вероятности ошибок по байтам по схеме Бернулли : %4.2f.\n', P_ERR(4, count)); P_ERR(4, count) = 1 - P_ERR(4, count); |
12 |
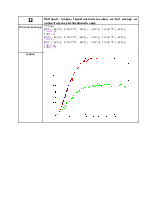
Построить график тероетической ошибки на бит исходя из корректирующей способности кода |
|
Исполняемый код |
figure; plot(P_ERR(1, 1:length(P_ERR)), P_ERR(2, 1:length(P_ERR)), 'green'); hold on; plot(P_ERR(1, 1:length(P_ERR)), P_ERR(3, 1:length(P_ERR)), 'red'); plot(P_ERR(1, 1:length(P_ERR)), P_ERR(4, 1:length(P_ERR |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.