Дополненная реальность (Augmented Reality, AR). Технологии реализация дополненной реальности, страница 3

Но в качестве исходных данных, как правило будет выступать как раз таки I, а n и M будут параметрами которые необходимо подобрать оптимальным образом.

Если с n все очевидно - размер алфавита маркеров, то M будет зависеть от размерности маркера, причем зависимость предстоит выяснить.

Изменение количества сегментов маркера

Как уже ранее оговаривалось, маркер является двумерной бинарной матрицей. Переписав такую матрицу в одну строку, мы получим число в двоичной системе счисления с количеством разрядов равной m*m, где m – размерность матрицы.

Тогда количество информации будет рассчитываться как:

M=2^m2,(2)

Где M – объем информации маркера.

Но следует помнить, что речь идет о квадратной матрице, которая будет иметь несколько степеней свободы в пространстве, а следовательно и по оси перпендикулярной объективу устройства захвата изображения. Это означает, что не все комбинации из (2) будут уникальными. Поворот матрицы на 90, 180, 270 градусов не даст новых комбинаций, а будет распознаваться как одна и та же. Так на (рис. 2) изображены одинаковые с точки зрения распознавания матрицы:

Рис.2 Матрицы идентичны.

Поэтому формула (2) будет являться ошибочной для расчета. Для вывода правильной формулы расчета проанализируем уникальные комбинации сегментов на небольших размерностях, то есть где есть возможность их просто подсчитать. Рассмотрим матрицу с размерностью m=2 и путем перебора найдем только уникальные комбинации:

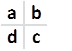
Получив таким образом 6 вариантов, проанализируем их относительно всех возможных комбинаций без учета поворота. Для этого выпишем их в виде двоичных чисел в следующую таблицу:

Т – развернутая матрица (abcd);

p – количество идентичных матриц с учетом поворота;

“+” перед  p означает уникальность матрицы относительно предыдущих матриц в таблице, с учетом поворотов;

“-”  – матрица является идентичной относительно одной из предыдущих в таблице.

Заметим, что 2 идентичные матрицы ( p = 2 ) имеют те матрицы, которые имеют симметричные сегменты по одной из диагоналей и отраженные по другой. Другими словами матрица при повороте на 0 градусов равна матрице с поворотом на 180, а матрица с углом поворота на 90 равна матрице с 270.

Матрицы, для которых p = 4 не имеют ни одного повтора при повороте на 90, 180, 270 градусов. А те, что имеют p = 1  наоборот равны для всех из четырех углов.

Из этих рассуждений следует, что количество уникальных матриц с параметром  p = 1 можно вычислить как:

MV₁ = 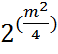, где m – размерность матрицы.