

.1.3 Обобщенный ряд Фурье
Система
тригонометрических функций, по которым производится разложение сигнала ![]() в ряд Фурье (1.5), не
является единственно возможной. В общем случае разложение сигнала в ряд может
быть выполнено по произвольным функциям
в ряд Фурье (1.5), не
является единственно возможной. В общем случае разложение сигнала в ряд может
быть выполнено по произвольным функциям ![]() . Так, если ставится задача представления
сигнала
. Так, если ставится задача представления
сигнала ![]() на
интервале [T1, T2] рядом вида
на
интервале [T1, T2] рядом вида 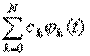 с наименьшей погрешностью
с наименьшей погрешностью
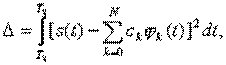
то коэффициенты ![]() могут быть найдены из
системы линейных уравнений
могут быть найдены из
системы линейных уравнений
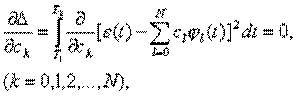
имеющей
единственное решение, если функции ![]() линейно независимы. При этом процесс
нахождения коэффициентов
линейно независимы. При этом процесс
нахождения коэффициентов ![]() оказывается наиболее простым, если исходная
система функций
оказывается наиболее простым, если исходная
система функций ![]() является
ортогональной, т.е.
является
ортогональной, т.е.
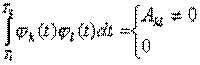
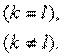
С помощью
соответствующей нормировки функций ![]() всегда можно обеспечить выполнение
условия:
всегда можно обеспечить выполнение
условия:
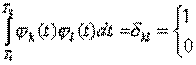
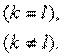
Такая система функций ![]() называется
ортонормированной. При этом
называется
ортонормированной. При этом
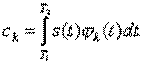
Если путем
увеличения N величина ![]() может
быть сделана сколь угодно малой, система функций
может
быть сделана сколь угодно малой, система функций ![]() называется замкнутой. При этом имеет
место равенство
называется замкнутой. При этом имеет
место равенство
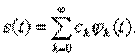
Такой ряд называют
сходящимся в среднем, а систему функций ![]() - базисной системой.
- базисной системой.
Если
сигнал ![]() и
функции
и
функции ![]() обладают
конечной энергией на интервале [T1, T2], что
практически всегда имеет место в рассматриваемых приложениях, замкнутость
базисной системы означает также ее полноту. Напомним, что система
ортогональных функций
обладают
конечной энергией на интервале [T1, T2], что
практически всегда имеет место в рассматриваемых приложениях, замкнутость
базисной системы означает также ее полноту. Напомним, что система
ортогональных функций ![]() называется
полной, если не существует функции, ортогональной всем функциям данной системы
и не равной тождественно нулю. При этом всякая полная система является
замкнутой.
называется
полной, если не существует функции, ортогональной всем функциям данной системы
и не равной тождественно нулю. При этом всякая полная система является
замкнутой.
Разложение
по ортонормированной системе базисных функций называется обобщенным рядом
Фурье, а набор коэффициентов ![]()
![]() часто называют спектром функции
часто называют спектром функции ![]() в соответствующем базисе.
в соответствующем базисе.
В зависимости от специфики решаемой задачи применяются различные системы базисных функций. Рассмотрим в качестве примера наиболее часто употребляемые базисные. В частности, используются разложения по полиномам Лежандра, Чебышева, Лагерра, Эрмита, функциям Хаара и Уолша и т.п.
Вообще любая система линейно независимых функций может быть ортогонализирована, т.е. с помощью соответствующих линейных комбинаций функций исходной неортогональной системы всегда можно получить систему ортогональных функций. Известно большое число различных способов такой ортогонализации, наиболее простым из которых является способ Шмидта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.