Adapted from slides by Lada Adamic, UMichigan
Outline
nn Small world phenomenon
nn Milgram’s small world experiment
nn Small world network models:
 |
nn Small world networks: why do they arise? nn efficiency nn navigation
Small World Phenomenon:
Milgram’s Experiment
Instructions:
Given a target individual (stockbroker in Boston), pass the message to a person you correspond with who is “closest” to the target.
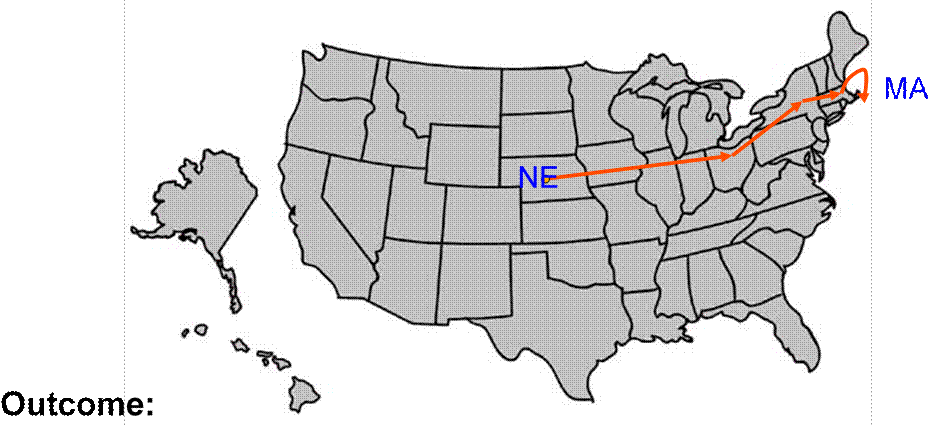
20% of initiated chains reached target average chain length = 6.5 ß “Six degrees of separation”
Source: undetermined
Small World Phenomenon:
Milgram’s Experiment Repeated
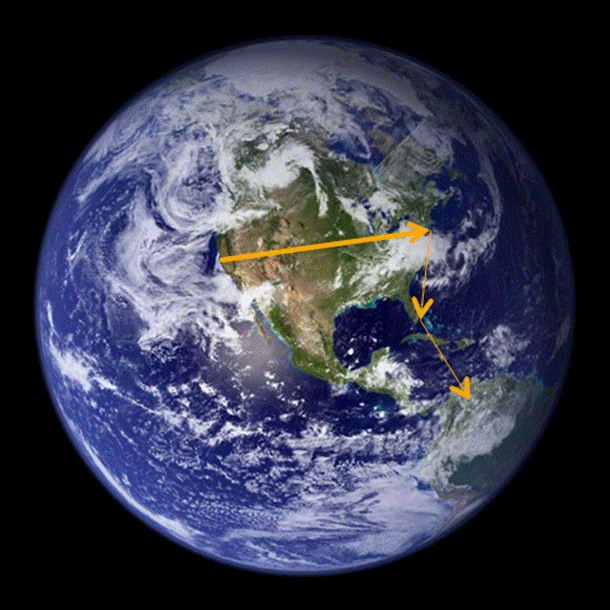email
experiment by
Dodds, Muhamad, Watts; Science 301, (2003)
(reading linked on website)
•18 targets
•13 different countries
•60 ,000+ participants
•24 ,163 message chains
•384 reached their targets
•Average path length = 4.0
Source: NASA, U.S. Government; http://visibleearth.nasa.gov/view_rec.php?id=2429
Small World Phenomenon:
nn Is 6 is a surprising number?
nn In the 1960s? Today? Why? nn If social networks were random… ?
nn Pool and Kochen (1978) - ~500-1500 acquaintances/person nn ~ 1,000 choices 1st link
nn ~ 10002 = 1,000,000 potential 2nd links nn ~ 10003 = 1,000,000,000 potential 3rd links
nn If networks are completely cliquish:
nn all my friends’ friends are my friends nn What would happen?
Small world experiment:
nn Is 6 an accurate number?
nn What bias is introduced by uncompleted chains? nn are longer or shorter chains more likely to be completed? nn if each person in the chain has 0.5 probability of passing the letter on, what is the likelihood of a chain being completed nn of length 2? nn of length 5?
Small world experiment accuracy:
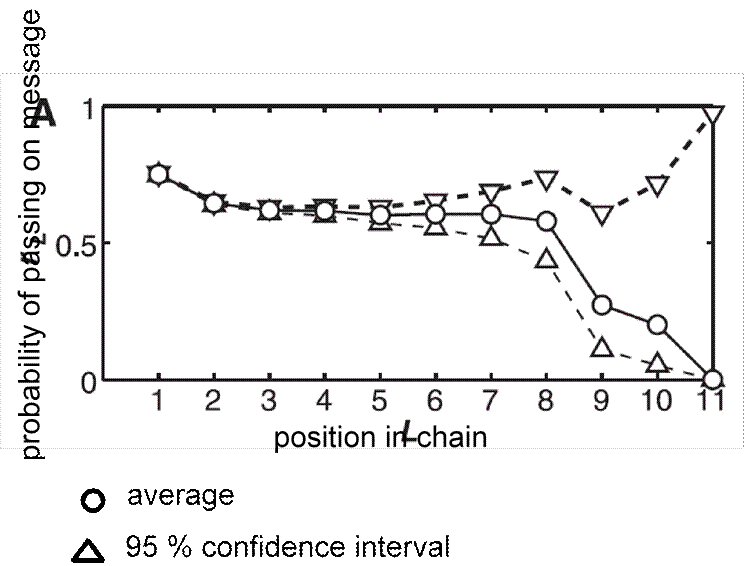
Source: An Experimental Study of Search in Global Social Networks: Peter Sheridan Dodds, Roby Muhamad, and Duncan J. Watts (8 August 2003); Science 301 (5634), 827.
nn observed chain lengths
nn ‘recovered’ histogram of path lengths
inter-country intra-country
Source: An Experimental Study of Search in Global Social Networks: Peter Sheridan Dodds, Roby Muhamad, and Duncan J. Watts (8 August 2003); Science 301 (5634), 827.
Small world experiment:
nn Is 6 an accurate number?
nn Do people find the shortest paths? nn Killworth, McCarty ,Bernard, & House (2005, optional): nn less than optimal choice for next link in chain is made ½ of the time
nn Facebook's data team released two papers in Nov. 2011 nn 721 million users with 69 billion friendship links nn Average distance of 4.74
nn Twitter studies nn Sysomos reports the average distance is 4.67 (2010) nn 50% of people are 4 steps apart, nearly everyone is 5 steps or less
nn Bakhshandeh et al. (2011) report an average distance of 3.435 among 1,500 random Twitter users
Business applications?
“Social Networking” as a Business:
• Facebook, Google+, Orkut, Friendster entertainment, keeping and finding friends
• LinkedIn:
•more traditional networking for jobs
• Spoke, VisiblePath
•helping businesses capitalize on existing client relationships
Same pattern:
high clustering Cnetwork >>Crandom graph
low average shortest path lnetwork ≈ ln(N)
"
neural network of C. elegans, " semantic networks of languages, "
actor collaboration graph " food webs
Reconciling two observations:
• High clustering: my friends’ friends tend to be my friends
• Short average paths
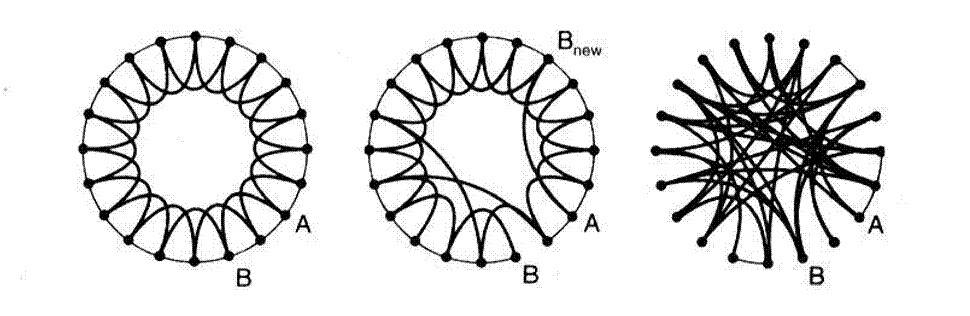
Source: Watts, D.J., Strogatz, S.H.(1998) Collective dynamics of 'small-world' networks. Nature 393:440-442.
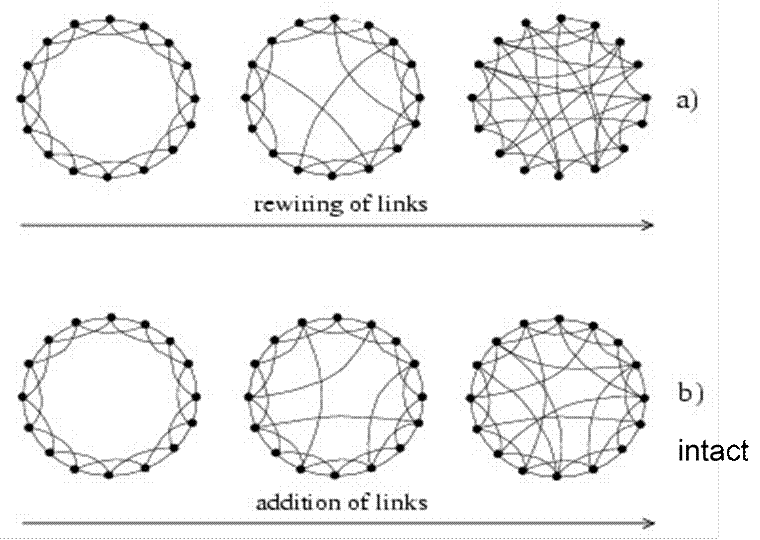Select
a fraction p of edges
Reposition one of their endpoints
Add a fraction p of additional edges leaving underlying lattice
nn As in many network generating algorithms nn Disallow self-edges nn Disallow multiple edges
Source: Watts, D.J., Strogatz, S.H.(1998) Collective dynamics of 'small-world' networks. Nature 393:440-442.
Watts-Strogatz model:
nn Each node has K>=4 nearest neighbors (local) nn tunable: vary the probability p of rewiring any given edge nn small p: regular lattice nn large p: classical random graph
Watts/Strogatz model:
What happens in between?
nn Small shortest path means small clustering? nn Large shortest path means large clustering?
nn Through numerical simulation nn As we increase p from 0 to 1 nn Fast decrease of mean distance nn Slow decrease in clustering
nn Clustering coefficient for graph:
Each triangle gets
#
triangles x 3 counted 3 times
# connected triples
nn Also known as the “fraction of transitive triples”
nn Clustering for node v:
# actual edges between neighbors of v
# possible edges between neighbors of v
nn Number of possible edges between k vertices:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
