Описание процесса функционирования системы. Нагруженный и ненагруженный резерв. Методы расчета надежности системы

Содержание:

1.Описание процесса функционирования системы.. 3

2. Методы  расчета надежности системы.. 4

2.1. Метод интегральных уравнений. 4

2.1.1.Расчет надежности системы.. 4

2.2. Метод дифференциальных уравнений. 8

2.2.1.Расчет надежности системы.. 8

Вывод. 11

1.Описание процесса функционирования системы

Система состоит из 3 однотипных усилителей с одним ненагруженным (в другом случае, нагруженным) резервным элементом.

Функционирование системы с ненагруженным резервом:

В системе работает 2 усилителя, один находится в резерве. После отказа в случайный момент t основного усилителя, подключается резерв и происходит его восстановление, но он не восстанавливается до конца (во втором случае восстанавливается и подключается опять в систему).

Функционирование системы с нагруженным резервом:

В системе работает 3 усилителя, одним из которых является резервный. Отказав в случайный момент t усилитель, начинает восстанавливаться, но не восстанавливается до конца (во втором случае восстанавливается и подключается опять в систему).

Суммарная длительность восстановления подчиняется экспоненциальному закону с параметром  μ. Интенсивность отказов усилителей  и  резервного элемента  при экспоненциальном законе надежности λ.

2. Методы  расчета надежности системы

2.1. Метод интегральных уравнений

Метод интегральных уравнений используется для расчета надежности как невосстанавливаемых, так и восстанавливаемых систем с любым законом распределения времени безотказной работы.

Надежность системы будет равна сумме вероятностей нахождения системы в работоспособных состояниях.

Для определения вероятности нахождения системы в том или ином состоянии, строится диаграмма состояний. На каждой из которых отмечается последовательность событий, приводящих систему на конец интервала времени t в рабочее состояние.

Используем  данный подход для расчета надежности восстанавливаемой системы с ненагруженным (нагруженным) резервом.

2.1.1.Расчет надежности системы

n=3 ; λ=10^-4 1/час ; µ=10^-11/час

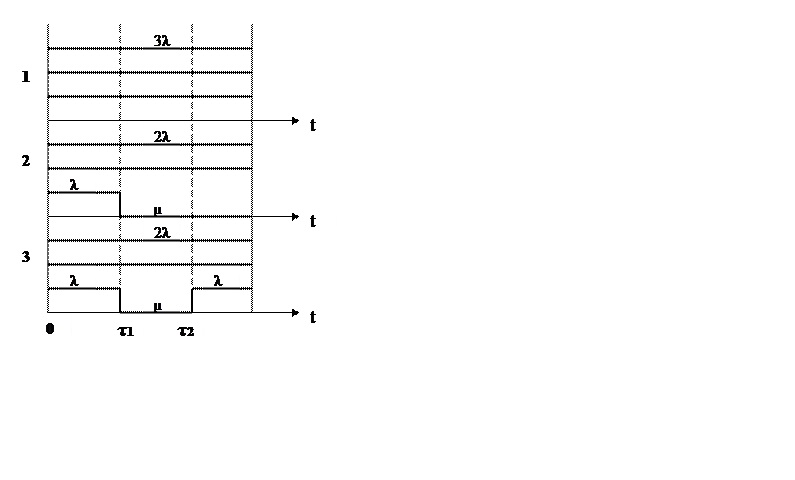
Рис.2.1.1.1 Диаграмма состояний (нагруженный резерв)

Состояние 1:

Все три усилителя не отказали на интервале [0,t] – P₁(t)- вероятность этого события

Состояние 2:

Два усилителя проработали безотказно на интервале [0,t]. Третий усилитель отказывает в случайный момент t1, который принадлежит интервалу [0,t], затем в случайный момент t1 происходит восстановление, но до конца усилитель не восстанавливается – P₂(t)- вероятность этого события.

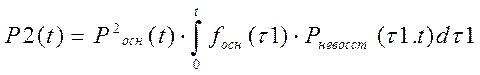,где

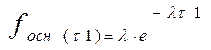  -   плотность распределения вероятности отказа основного элемента

- вероятность безотказной работы устройств, не отказавших на интервале [0,t].

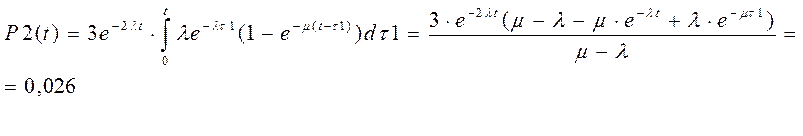  Состояние 3:

Два усилителя проработали безотказно на интервале [0,t]. Третий усилитель отказывает в случайный момент t1, который принадлежит интервалу [0,t] и в случайный момент t1 происходит восстановление на интервале [τ1,τ2]. Затем в случайный момент τ2 восстановленный усилитель включается опять в систему . – P₂(t)- вероятность этого события.

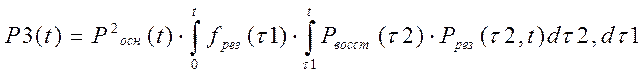, где

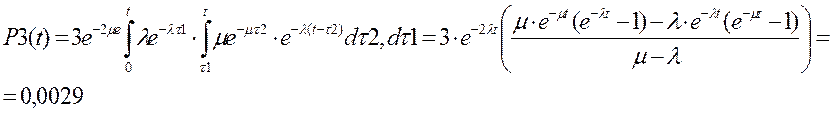
n=3 ; λ=10^-4 1/час ; µ=10^-11/час

	1
	2
	3

 

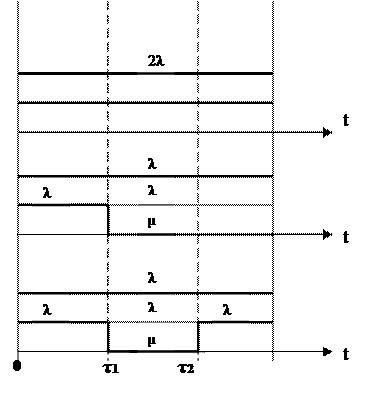
Рис.2.1.1.2 Диаграмма состояний (ненагруженный резерв)

Состояние 1:

Два усилителя не отказали на интервале [0,t] – P₁(t)- вероятность этого события

Состояние 2:

Один усилитель проработал безотказно на интервале [0,t]. Второй усилитель отказывает в случайный момент t1, который принадлежит интервалу [0,t] и на его место включается резерв. Затем в случайный момент t1 происходит восстановление , но до конца усилитель не восстанавливается – P₂(t)- вероятность этого события.

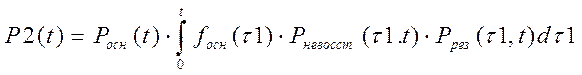,где

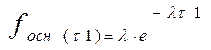  -   плотность распределения вероятности отказа основного элемента

- вероятность безотказной работы устройств, не отказавших на интервале [0,t].

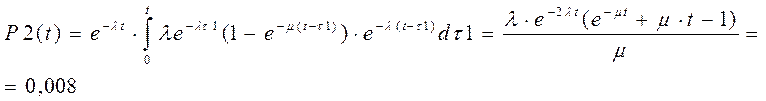
Состояние 3:

Один усилитель проработал безотказно на интервале [0,t]. Второй усилитель отказывает в случайный момент t1, который принадлежит интервалу [0,t] и на его место включается резерв. Затем в случайный момент t1 происходит восстановление отказавшего усилителя на интервале [τ1,τ2]. Достигнув момента τ2 восстановленный усилитель включается опять в систему . – P₂(t)- вероятность этого события.

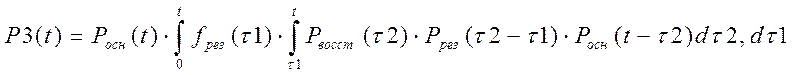    где

2.2. Метод дифференциальных уравнений

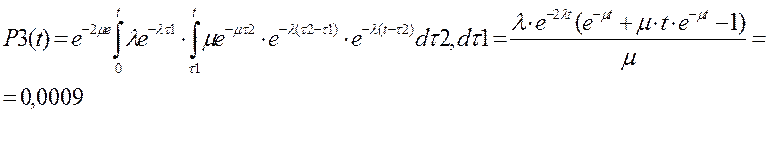
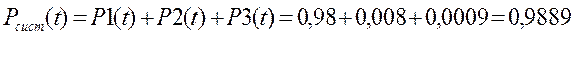
Этот метод используется для расчета надежности как восстанавливаемых, так и невосстанавливаемых систем. Закон распределения вероятности безотказной работы элементов системы должен быть только экспоненциальным P(t)=e^-lt   или  P_обсл(t)=e^-μt  .

Состояния в системе будем различать по числу отказавших элементов.

Для начала строится граф состояний, далее составляется система дифференциальных уравнений. Каждое уравнение определяет вероятность нахождения системы в одном из выделенных состояний.

2.2.1.Расчет надежности системы

n=3 ; λ=5·10^-2 1/час ; µ=5·10^-11/час

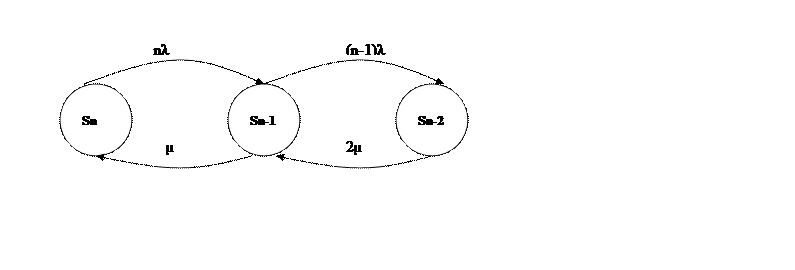
Рис.2.2.1.1. Граф состояний (нагруженный резерв)

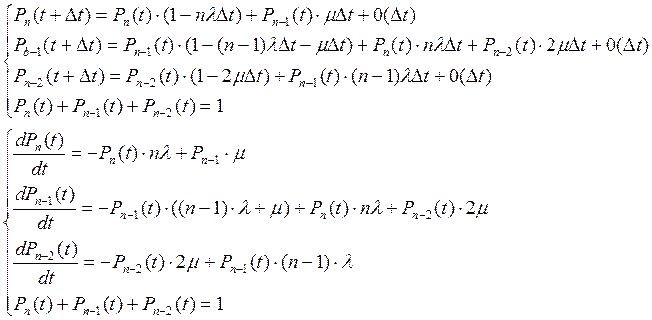
Распишем одно из уравнений (первое):

Вероятность нахождения системы в момент времени  в состоянии  Sn равна сумме вероятностей трех событий:

Или в момент времени   система находится в состоянии Sn , вероятность отказа которого- или момент времени   система находится в состоянии Sn-1 , вероятность восстановления которого-  и на интервале  не откажет ни один из работающих усилителей-.

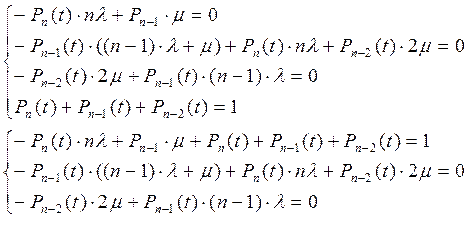
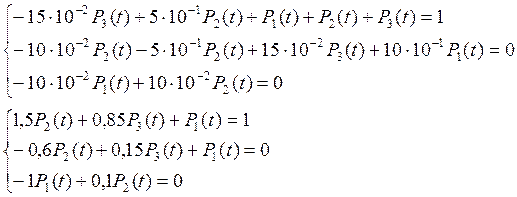
Решим полученную систему методом Крамера:

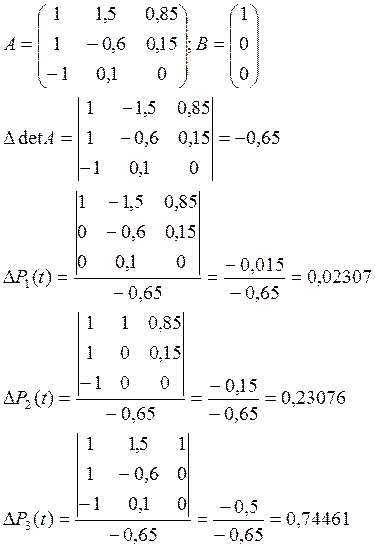
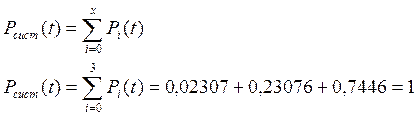
n=3 ; λ=5·10^-2 1/час ; µ=5·10^-11/час

 

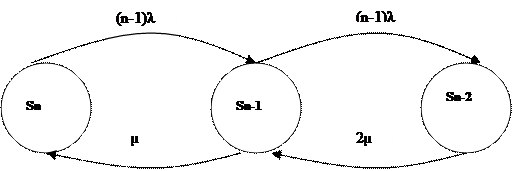Рис.2.2.1.2. Граф состояний (ненагруженный резерв)

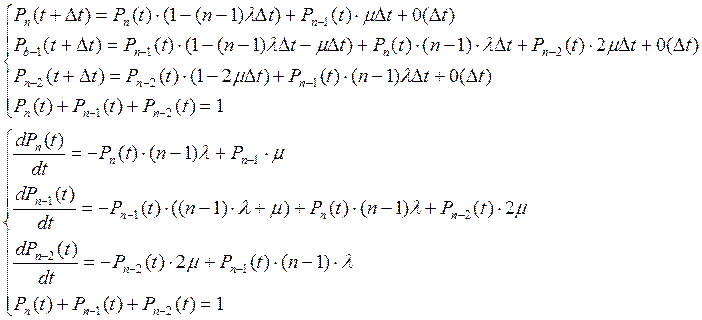
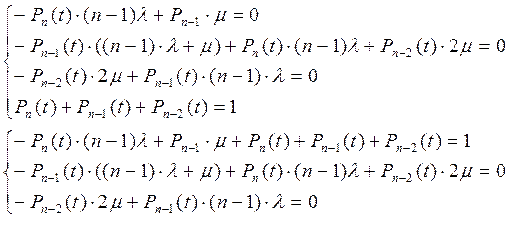
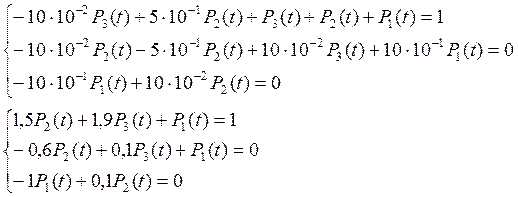
Решим полученную систему методом Крамера:

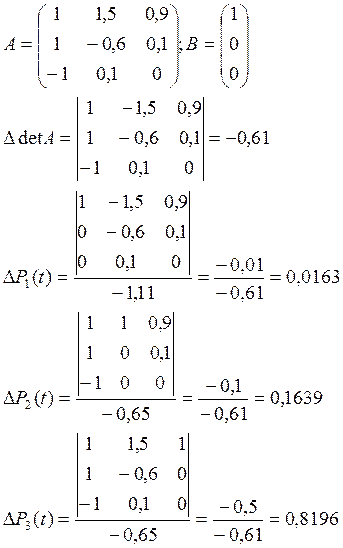
Вывод:

В методе интегральных уравнений мы рассматривали только те состояния , в которых система будет находиться в рабочем состоянии, а в методе дифференциальных уравнений  рассматривали состояния, в которых все элементы системы работоспособны в момент t=0 и на интервале времени Dt может произойти некоторые события. Состояния в системе различали по числу отказавших элементов

Результаты получились практически одинаковыми.