Это нововведение облегчило создание моделей, так как ранее (например, в среде GPSS PC) данные функции задавались как непрерывные (дискретные, по необходимости) с помощью команды FUNCTION и перечислением большого числа точек (обычно около 25), что обусловлено методом интерполяции значений непрерывной функции в языке GPSS.
Так, например, в среде GPSS World можно задать функцию экспоненциального распределения с помощью библиотечной функции EXPONENTIAL(A,B,C), где A – номер генератора случайных чисел, B – коэффициент сдвига и C – коэффициент масштабирования. Причём известно, что квадрат коэффициента C равен значению дисперсии этой функции, а сумма операндов B и C – математическому ожиданию. Таким образом, можно легко подобрать необходимые для проведения опыта значения функции.
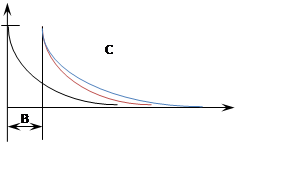
Рисунок 1
В отличие от распространённой формулы, плотность экспоненциального распределения в GPSS описывается с использованием двух коэффициентов и выглядит так:
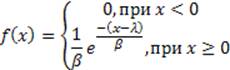
Как раз из этой формулы и выводится зависимость между операндами библиотечной функции и такими параметрами как математическое ожидание и дисперсия.
Рассмотрим варианты использования функции распределения. Например, известно, что покупатели приходят в магазин каждые 6 минут, плюс-минус 3 минуты. Это условие можно задать различными способами.
Во-первых, самым простым. Стандартным способом – с помощью точного определения операндов A и B в блоке GENERATE. Тогда строка будет выглядеть так:
GENERATE 6,3
Это же условие можно задать с помощью непрерывной функции, тогда код будет выглядеть так:
TimeDelay FUNCTION RN12,C2
0,3/1,9
GENERATE FN$TimeDelay
При этом надо учитывать, что с помощью генератора случайных чисел можно получить числа из диапазона от 0 до 0,999999, т.е. единица никогда не будут сгенерирована.
Но, с точки зрения статистики, было бы более верно задать это условие с помощью экспоненциальной функции распределения. Без дополнительных библиотечных функций определение плотности экспоненциального распределения выглядело бы примерно так:
TimeDelay FUNCTION RN12,C25
0,3/.1537,3/.2836,3.5/.3931,4/.4861,4.5/.5650,5/.6317,5.5/.6886,6/.7364,6.5/.7773,7/.8122,7.5/.8411,8/.8655,8.5/.8861,9/.9039,9.5/.9186,10/.9310,10.5/.9416,11/.9505,11.5/.9582,12/.9701,13/.9845,15/.9920,17/.9971,20/1,24
GENERATE FN$TimeDelay
А чтобы задать функцию распределения с такой же плотностью, используя библиотечную функцию, необходимо вначале рассчитать операнды B и C. Для чего составим и решим систему уравнений:
Так как, по заданию, Mx ≈ 6, а σ ≈ 3, то получаем следующую систему:
Решив её и определив значения параметров, составим функцию:
GENERATE (EXPONENTIAL(12,3,3))
Надо учитывать, что оболочка GPSS World может оперировать с вещественными числами в диапазоне 
до 
, но с
точностью (приблизительно) до 15 знака после запятой. Это необходимо знать, при
передаче различных параметров.
Также стоит заметить, что при задании интервалов с помощью явных значений атрибутов происходит генерация интервалов распределённых по равномерному закону.
Иначе говоря, записи
GENERATE 6,3
и
GENERATE (UNIFORM(1,3,9))
идентичны по результату работы.
Проверить плотность распределения можно, построив диаграмму, где по оси абсцисс будут расположены интервалы появления транзактов. Для построения диаграммы нужно выполнить следующий код, написанный на языке GPSS:
TimeDelay_Tab TABLE V$TimeDelay_Var,2.5,0.5,60
TimeDelay_Var VARIABLE C1-X1
GENERATE (Exponential(200,3,3))
TABULATE TimeDelay_Tab
SAVEVALUE 1,C1
TERMINATE
GENERATE 1000000
START 1
TERMINATE 1
Сегодня я уже неоднократно говорил о "библиотечных" функциях. Дело в том, что функции распределения не являются частью самого языка GPSS, а относятся к функциям расширения оболочки GPSS World. Все функции расширения относятся к PLUS. PLUS – это аббревиатура, которая на английском звучит как The Programming Language Under Simulation и переводится на русский язык фразой: Язык программирования для моделирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.