


3.2. Связь выходного и входного сигналов линейной системы.
Рассмотрим линейную инвариантную во времени систему.
Система является линейной, если она удовлетворяет принципу
суперпозиции. Согласно принципу суперпозиции, если yi(t)
- это выходной сигнал (реакция) системы при входном сигнале xi(t),
то при входном воздействии в виде линейной комбинации 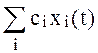 реакцией
системы будет
реакцией
системы будет 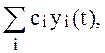 т.е. линейная комбинация
отдельных реакций.
т.е. линейная комбинация
отдельных реакций.
Инвариантной во времени (стационарной) называют систему, удовлетворяющую следующему условию. Пусть y(t) представляет собой реакцию системы на входной сигнал x(t), т.е. x(t)®y(t). Тогда сдвиг во времени входного сигнала системы должен вызывать такой же сдвиг выходного сигнала, т.е. x(t-t)®y(t-t) для -¥ < t < ¥. Обычно линейные инвариантные во времени системы для краткости называют просто линейными, уточняя при необходимости свойство инвариантности. Общий вид такой системы в виде “черного ящика”, имеющего вход и выход, показан на рис. 3.3.
![]()
![]() x(t)
x(t)
|
Рис. 3.3. Общее представление линейной системы
Линейными нестационарными (параметрическими) являются системы с переменными параметрами. У таких систем хотя бы один параметр изменяется с изменением времени и , следовательно, свойство инвариантности во времени для них несправедливо. Линейные стационарные системы описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами, линейные нестационарные - обыкновенными дифференциальными уравнениями с переменными коэффициентами.
Реакция (выходной сигнал) линейной системы при входном сигнале в виде d-функции (единичной импульсной функции) называется импульсной переходной характеристикой или весовой функцией системы. Будем обозначать ее через w(t) (рис.3.4).
|
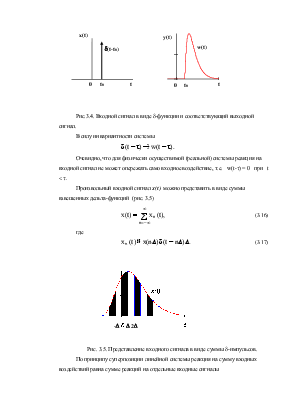
Рис.3.4. Входной сигнал в виде d-функции и соответствующий выходной сигнал.
В силу инвариантности системы
![]()
Очевидно, что для физически осуществимой (реальной) системы реакция на входной сигнал не может опережать само входное воздействие, т.е. w(t-t) = 0 при t < t.
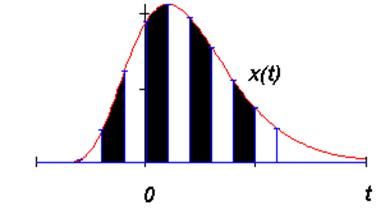
Произвольный входной сигнал x(t) можно представить в виде суммы взвешенных дельта-функций (рис. 3.5)
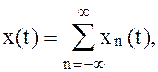 (3.16)
(3.16)
где
![]() (3.17)
(3.17)
|
Рис. 3.5. Представление входного сигнала в виде суммы d-импульсов.
По принципу суперпозиции линейной системы реакция на сумму входных воздействий равна сумме реакций на отдельные входные сигналы
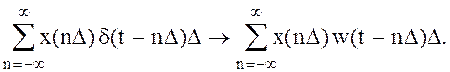 (3.18)
(3.18)
При D®0 в пределе получим выражение
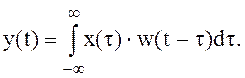 (3.20)
(3.20)
Это выражение называется интегралом свертки (интегралом наложения) и играет исключительно важную роль в теории и практическом использовании линейных систем.
Уравнение свертки имеет и другие формы, например,
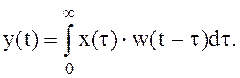 (3.21)
(3.21)
Здесь предполагается, что x(t)= 0 при t < 0. Если учесть также свойство физической осуществимости (каузальности) системы, означающее, что для реальной системы w(t - t) = 0 при t < t, то
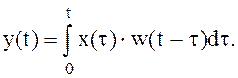 (3.22)
(3.22)
Все эти три эквивалентных выражения можно записать также символически в виде свертки
![]() (3.23)
(3.23)
Операция свертки означает, что значение выходного сигнала линейной системы в момент t зависит не только от значений x(t) и w(t) в момент t, но и от всех значений в предшествующие моменты времени (предыстории).
В п.2.6 показано, что свертке во временной области соответствует произведение преобразований Фурье в частотной области, т.е.
![]() (3.24)
(3.24)
где
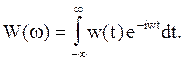 (3.25)
(3.25)
амплитудно-фазовая частотная характеристика (функция, комплексный коэффициент передачи) линейной системы. Она представляет собой реакцию системы на входное воздействие в виде комплексной гармоники eiwt.
Действительно, выход системы
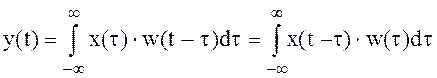 , при
, при ![]()
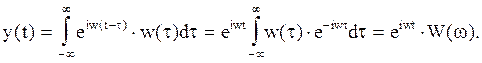 (3.26)
(3.26)
Модуль |W(w)\ называется амплитудно-частотной характеристикой системы и отражает изменение амплитуды гармонического сигнала при прохождении его через линейную систему.
Аргумент arg W(w) представляет фазо-частотную характеристику системы и характеризует изменение фазы гармоники на выходе системы.
Операция умножения проще, чем интегрирование по уравнению свертки, поэтому преобразование сигнала в частотной области, сводящееся к обычному перемножению X(w) и W(w), является обычным инструментом анализа линейных систем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.