Уравнение Максвелла. Принцип взаимности. Решение для метода комплексных амплитуд. Сферическую систему координат

12. Большинство задач электродинамики разделяют на внутренние краевые задачи и внешние. Для внутренней задачи требуется найти решение внутри замкнутого объема V₁ , ограниченного поверхностью S. Во внешней задаче ищется решение вне объема V₁ . Теорема единственности для внутренней задачи утверждает, что внутри объема V₁ ,ограниченного поверхностью S, решение уравнений Максвелла для комплексных амплитуд.

 ;  

единственно, если во-первых, оно удовлетворяет одному из трех краевых условий:

1. заданным на поверхности S значением тангенциальной составляющей вектора ; 2. заданным на поверхности S значением ; 3.заданным на части поверхности S значением , и на остальной части S значением ,

-  и если во-вторых, при отсутствии потерь (s=0) частота w не совпадает ни с одной из резонансных частот области V_1. Если при s=0 частота совпадает с одной из резонансных частот, решение будет неоднозначным.

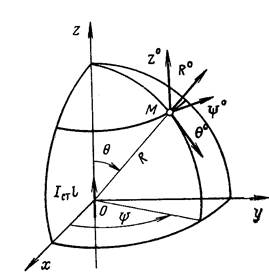
Единственность решения внешней задачи доказывается при условии, что все сторонние источники распределены на конечном расстоянии от начала координат. Внешняя задача решается для безграничного объема V, ограниченного поверхностью S, исключающей внутренний объем V₁, и бесконечной удаленной поверхности S_¥.(рисунок 2.3).

Условия единственности решения внешней задачи:

1. на поверхности S таким же условиям, что и при решении внутренней задачи;

2. в среде без потерь (s=0) при R®¥ условием излучения (4.1);

3. в среде с потерями (s¹0) условием на бесконечности.

Условия излучения:

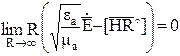
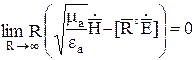
конечной величине; конечной величине. Физически условия излучения означают, что на больших расстояниях от источников, создаваемые ими поля имеют характер сферических бегущих волн, расходящихся от источников в радиальных направлениях. Амплитуды векторов поля  и волн убывают на больших расстояниях от источников по закону . В безграничной среде с потерями (s¹0) условия излучения заменяют условиями на бесконечности:           ;                                          

Они означают, что при наличии потерь векторы поля на больших расстояниях от источников убывают быстрее чем , то есть ,  где a - положительное число.

В реальных условиях удельная проводимость s¹0, поэтому R®¥, .

13.  Принцип двойственности. Магнитных зарядов в природе не существует, но для облегчения расчетов они вводятся. Принцип перестановочной двойственности заключается в том, что перестановки: , , , и , , , преобразуют систему  и  в   и  и наоборот. Если известно решение для электрических источников, то используя замену можно без решения задачи получить решение для магнитных источников.

Принцип взаимности:

Если распределения токов в объеме V₁ одинаково с таковым   в объеме V₂, то и одинаковы создаваемые ими электрические поля .

Принцип эквивалентности источников. Пусть реальные источники расположены в объеме V₁, ограниченном поверхностью S, они могут быть неизвестными или заданы сложной зависимостью, но предполагаются известными значения касательных составляющих создаваемого ими поля  и  на поверхности S. Этого достаточно, согласно теореме единственности, для нахождения ЭМП вне объема V_1. Касательные составляющие  и  можно выразить через эквивалентные им поверхностные токи  и электрические и магнитные. Эти поверхностные токи называют эквивалентными источниками, их можно рассчитать или измерить на любой поверхности S, окружающей истинные источники . Плотность эквивалентного электрического тока определяется касательной составляющей вектора , а плотность эквивалентного магнитного тока – касательной вектора : ;                                  

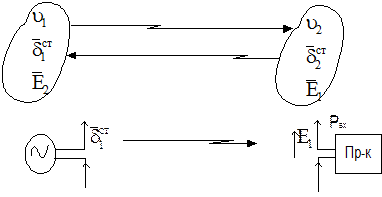14.  Применим к первому уравнению Максвелла операцию ротора: , так как получим: 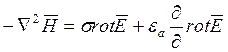. Применив второе уравнение Максвелла для  получим: 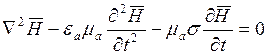. И 2е уравнение .

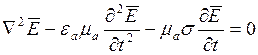В случае монохроматического ЭМП , 

k² – волновое число. Для нахождения векторов поля сначала вводят вспомогательные функции, а затем через них вычисляют векторы поля. Эти вспомогательные функции называются электродинамическими потенциалами. Введем их: , =>  и , где  - векторный электродинамический потенциал