Микропроцессоры семейства ADSP21xx. Структура микропроцессорного ядра ADSP21xx. Принцип рекурсивной фильтрации

Внутренняя архитектура построена вокруг этой концепции для эффективной реализации DSP–приложений, так как реализация разностных уравнений для СС ФЗ фильтров требует использования операций умножения/накопления с последовательным сохранением данных. Одна инструкция умножения помещена внутри цикла для того, чтобы эффективно реализовать фильтр.

 

2.1 Принцип рекурсивной фильтрации

Конструкция РЦФ отображается в z–образе передаточной функции фильтра в виде отношения двух многочленов:

H(Z) = H0+H1Z+H2Z²+…= B(Z)/[1+A(Z)],                              (1)

где: B(Z) = B0+B1Z+B2Z²+…+BNZ^N, 

 A(Z) = A1Z + A2Z² +…+AMZ^M.

Естественно, что переход на РЦФ имеет смысл только в том случае, если степень многочленов A(Z) и B(Z) во много раз меньше степени многочлена H(Z) прямого z–преобразования импульсной реакции фильтра. При z–образе входных данных  X(Z), на выходе РЦФ имеем:

Y(Z) = H(Z) X(Z) = X(Z) B(Z)/[1+A(Z)],

Y(Z)/[1+A(Z)] = Y(Z) + Y(Z) A(Z) = X(Z) B(Z),

Y(Z) = X(Z) B(Z) – Y(Z) A(Z).                                                          (2)

При обратном z–преобразовании выражение (2) получаем уравнение рекурсивной цифровой фильтрации:

y_k= b_nx_k-n –a_my_k-m                                   (3)

 

Z

– A(z)

                                                                         

Рисунок 3. Схема рекурсивной фильтрации.

Рекурсивная фильтрация требует задания начальных условий как по X_k, так и по y_k  при k<0. Схема рекурсивной фильтрации приведена на рисунке 3.

Как следует из выражения (3), при вычислении значения y_k текущей точки используются предыдущие вычисленные значения y_k-m, (m>0), что и определяет принцип рекурсии – фильтрации с обратной связью. Другой особенностью РЦФ является их односторонность и физическая реализуемость в реальном масштабе времени.

При машинной обработке данных многочлен B(Z) передаточной функции фильтра может реализоваться и в двухстороннем варианте.

Одно из важнейших свойств рекурсивных фильтров – возможность получения узких переходных зон при конструировании частотныхфильтров, так как функция H(Z)  фильтра может резко изменяться при приближении к нулю многочлена в знаменателе (1).

Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчётов для текущих вычислений может приводить к накапливанию ошибок.

Практическая реализация РЦФ осуществляется в двух вариантах.

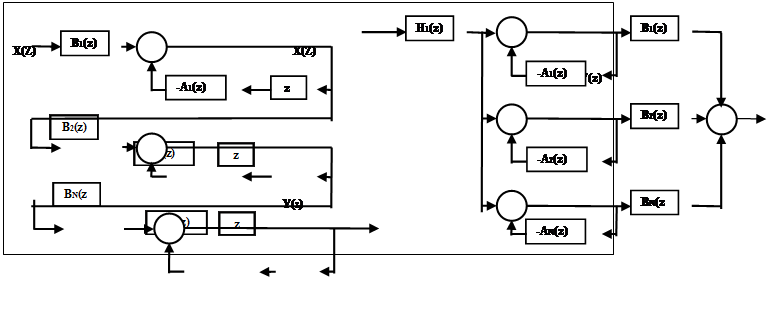Рисунок.4. Каскадная форма                      Рисунок.5. Параллельная форма

Каскадная форма. Находятся корни многочленов A(Z), B(Z) и производится разложение H(Z):

H(Z) = G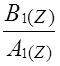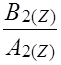…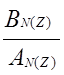,                             (4)

Где G - масштабный множитель. Это позволяет применять каскадное построение фильтров, показанное на рисунке 4, в котором:

H(Z) = G H₁(Z) H₂(Z)…H_N(Z),

H_n(Z) = B_n(Z)/A_n(Z)

Функции A_n(Z)  и B_n(Z) обычно представляются в виде биквадратных блоков (фильтров второго порядка):

B_n(Z) = b_n.0 + b_n.1z + b_n.2z²,

A_n(Z) = 1 + a_n.1z +a_n.2z²

Параллельная форма. Функция H(Z) разлагается на элементарные дроби:

H(z) = H₀(z) B_n(z)/[1 + A_n(z)], что даёт параллельную форму фильтра, показанную на рисунке 5. Параллельная конструкция фильтра применяется много реже каскадной, хотя это может объясняться и тем, что в аналоговых фильтрах, исторически предшествовавших цифровым фильтрам, теоретическая базаанализа и синтеза каскадных рекурсивных фильтров получила весьма детальное развитие.

Устранение сдвига фазы. Рекурсивные фильтры являются фазосдвигающими фильтрами. Если требуется обеспечить нулевой фазовый сдвиг, то операция фильтрации производится дважды, в прямом и обратном направлении числовой последовательности массива данных, при этом амплитудно – частотная  характеристика (АЧХ) фильтрации будет равна |H(w)|² фильтра, что необходимо учитывать при конструировании фильтра.

3. Расчетная часть

3.1 Реализация рекурсивного фильтра I-го порядка

В рассмотренней далее программе, используя имитатор, мы получили импульсную (рисунок ) и переходную (рисунок ) характеристики рекурсивного фильтра первого порядка (рисунок 6), заданного уравнением:

y(n) = b* x(n)+(1-b)* y(n -1)

                       x(n)                                                      y(n)

 

Z-1

                                           

 

                                         -b

Рисунок 6. Рекурсивный фильтр первого порядка.

Аналоговым прототипом такого фильтра является интегрирующая RC- цепь с постоянной времени =RC. Как известно, время установления t_у переходной характеристики RC- цепи составляет 2.2. В цифровом варианте 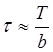, где Т – период следования отсчётов и равен он 1 мс.

Согласно нашего технического задания произведём расчёты:

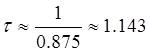мс

t_у =1.143 х 2.2 = 2.514 мс

Время установления t_у переходной характеристики можно проследить на графике рисунка .

Если x(n) – последовательность импульсов имеет вид дельта-функции (n), тогда выходная последовательность фильтра y(n) является импульсной характеристикой. Так, как эта последовательность бесконечная, программа вычисляет только несколько первых отсчётов. Когда последовательность x(n) имеет вид единичного скачка 1(t), выходная последовательность y(n) представляет собой переходную характеристику фильтра.

4. Блок – схема алгоритма реализации рекурсивного фильтра

Z=x - y Y=y + z х b

Samples-1 x=x+1 y=y+1 z=z+1

АУО = PM (I4:M4)

VAR dm_y VAR x_input

                                                                   Нет

Да

Вывод

                                                                                                                                                                         

Рисунок 7. Блок – схема алгоритма реализации рекурсивного фильтра

Заключение

Данный курсовой проект дал мне практические и теоретические знания в области цифровых сигнальных процессоров. На примере цифровых сигнальных процессоров  семейства ADSP-21XX