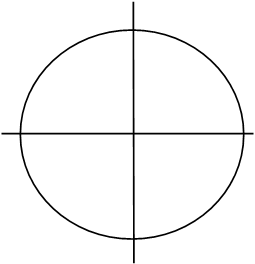
Данная аппроксимация точна для любого значения аргумента от 0о до 90о (первый квадрант), т.е. для 0<x<0.5. Т.к. sin(-j) = -sin(j) и sin(j) = sin (180o - j), синус любого угла можно выразить через синус угла первого квадранта. Границы квадрантов показаны на рисунке 5.1.
p/2
 0x4000 0x3FFF
0x4000 0x3FFF
0x7FFF 2 1 0x0000
p 0
0x8000 0xFFFF
3 4
0xBFFF 0xC000
-p/2
Рисунок 5.1. Масштабированные значения аргументов
|
-180O |
-90O |
0O |
90O 180O |
|
-1 |
-0.5 |
0 |
0.5 1.0 |
|
8000 BFFF |
C000 FFFF |
0000 3FFF |
4000 7FFF |
Таким образом, в этой задаче мы встречаемся с масштабированием как для аргумента x с коэффициетом p, так и для функции с коэффициентом 8.
Цифровой генератор гармонического сигнала
Подпрограмма SINE.DSP, реализующая данную аппроксимацию, приведена в файле Описание_ЛР5.docв приложении. Она принимает входные значения x в формате 1.15. Коэффициенты многочлена по абсолютной величине достигают величины 5.325196. Для их представления в программе выбран формат 4.12, допускающий диапазон представления чисел -8...8. Такое масштабирование позволяет отобразить диапазон значений, в котором находятся коэффициенты многочлена.
Подпрограмма читает масштабированное входное значение x из регистра АX0. Это значение модифицируется для перевода в первый квадрант. Если значение находится во втором или четвертом квадрантах (бит 14 входного значения равен 1), перемена знака (или инвертирование) переводит значение в первый или третий квадрант, соответственно.
Знаковый разряд затем сбрасывается для того, чтобы получить значение в первом квадранте; оно сохраняется в регистре AR.
Функция синус вычисляется путем умножения увеличивающихся степеней входного значения х на соответствующие коэффициенты. Квадрат аргумента вычисляется и сохраняется в MF, в то время, как сохраненный первый коэффициент загружается из памяти данных. Первый член аппроксимации сохраняется в регистре MR (в котором результат накапливается) параллельно с загрузкой второго коэффициента. В цикле approx вычисляется следующий член апроксимации и добавляется к предыдущему результату в MR; затем инструкция умножения загружает следующий коэффициент и формирует одновременно следующую степень аргумента x.??
Поскольку при вычислениях использованы коэффициенты в формате 4.12, необходима инструкция сдвига для масштабирования результата в формат 1.15. После этого результат проверяется на переполнение. Если значение в регистре SR1 превышает 0х7FFF, программа выполняет операцию насыщения до максимального положительного значения 0х7FFF, которое читается из регистра AY0. Затем, если необходимо, восстанавливается знаковый разряд. Если входной аргумент (сохраненный в АX0) отрицательный, результат тоже должен быть отрицательным.
Подпрограмма содержит новую директиву Ассемблера .GLOBAL. Она делает метку sin: видимой для других программ (особенно для главной программы), для использования в вызовах подпрограмм или переходов внутри программного модуля. Подпрограмма читает масштабированное входное значение x из регистра АX0. Это значение модифицируется для перевода в первый квадрант. Если значение находится во втором или четвертом квадрантах (бит 14 входного значения равен 1), перемена знака (или инвертирование) переводит значение в первый или третий квадрант, соответственно.
Знаковый разряд затем сбрасывается для того, чтобы получить значение в первом квадранте, которое сохраняется в регистре AR..
На вычисление одного значения синуса требуется 25 циклов. При тактовой частоте процессора 12,5 МГц одно значение синуса вычисляется за 2 мкс.
Главная программы MAIN, использующая подпрограмму sine, вычисляет одно значение sin(p/2). Она содержит директиву Ассемблера .EXTERN для связи подпрограммы и главной программы. Эта директива присваивает атрибут метке sin: как внешней, объявленной в другом модуле с использованием директивы .GLOBAL. Поэтому возникает возможность вызывать подпрограмму sine из главной программы. Так как исходный параметр, нужный этой подпрограмме, извлекается из регистра АX0, его приходится инициализировать перед вызовом подпрограммы. В регистре АX0 установлено значение аргумента 0х4000, которое соответствует углу p/2. После возврата из подпрограммы вычисленное значение синуса будет находиться в регистре AR в формате 1.15.
В заключение выполните программу. Убедитесь, что в регистре AR возникает корректное значение синуса p/2. Проверьте результаты работы программы ещё для нескольких значений аргумента как в первом, так и в других квадрантах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.