5. во всех областях
71
Пластины воздушного конденсатора раздвигают на расстоянии вдвое большее первоначального, а между пластинами помещают пластинку диэлектрика с относительной проницаемостью x=5. В результате ёмкость конденсатора:
1. увеличится в 2,5 раза=
2. уменьшится в 2,5 раза
3. увеличится в 10 раз
4. уменьшится в 10 раз
-16-
72
Пластины плоского конденсатора сближают на расстояние вдвое меньшее первоначального и вынимают пластину диэлектрика с относительной диэлектрической проницаемостью x=4. В результате ёмкость конденсатора:
1. увеличится вдвое
2. уменьшится вдвое=
3. увеличится в 8 раз
4. уменьшится в 8 раз
5. не изменится
73
Заряд на каждой из пластин конденсатора увеличили вдвое, а напряжение уменьшили вдвое. Ёмкость конденсатора:
1. не уменьшилась
2. уменьшилась в 4 раза
3. увеличилась в 4 раза=
4. уменьшилась в 2 раза
5. увеличилась в 2 раза
74
N конденсаторов одинаковой ёмкости C1 каждый сначала соединили параллельно, а затем последовательно. Результирующая ёмкость при замене параллельного соединения на последовательное:
1. уменьшилась в N2 раз=
2. увеличилась в N2 раз
3. уменьшилась в N раз
4. увеличилась в N раз
5. не изменилась
75
Два конденсатора ёмкостью X и ёмкостью 20 мкФ соединены последовательно. Общая ёмкость равна 4 мкФ. Значение X (мкФ) составляет:
1. 25 3. 15 5. 5=
2. 20 4. 10
-17-
76
Два одинаковых воздушных конденсатора одинаковой ёмкости C1, соединили последовательно. Затем один из конденсаторов заполняется жидким диэлектриком с относительной диэлектрической проницаемостью x=4. Общая ёмкость конденсаторов:
1. не изменится
2. увеличится в 1,6 раз=
3. уменьшится в 1,6 раз
4. увеличится в 4 раза
5. уменьшится в 4 раза
77
Пять одинаковых воздушных конденсатора ёмкостью 2 мкФ каждый соединяют параллельно. Затем в два конденсатора одновременно вводят диэлектрик с относительной диэлектрической проницаемостью: x1=2, x2=3. Общая ёмкость системы параллельно соединённых конденсаторов:
1. увеличится на 4 мкФ
2. не изменится
3. уменьшится на 6 мкФ
4. увеличится на 6 мкФ=
78
Конденсатор состоит из двух плоских круглых пластин радиусом R каждая. Пластины находятся на расстоянии d друг от друга в вакууме. Ёмкость такого конденсатора можно вычислить, как:
1.= 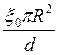 2.
2. 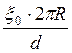 3.
3.
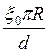 4.
4. ![]()
5. ![]()
-18-
79
Дана схема (рис1) соединения одинаковых конденсаторов ёмкостью 8 пФ каждый. Если изменить схему (рис2), то общая ёмкость:
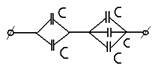 1. увеличится на 7,3 пФ
1. увеличится на 7,3 пФ
2. уменьшится на 7,3 пФ=
3. уменьшится на 37,7 пФ
![]() 4. увеличится на 37,7 пФ
4. увеличится на 37,7 пФ
5. не изменится
80
Ёмкость плоского конденсатора 20 мкФ, а напряжение на конденсаторе 100 В. Энергия электрического поля конденсатора составляет:
1. 0,001 Дж 2. 0,1 Дж= 5. 0,2 Дж
2. 0,01 Дж 3. 0,002 Дж
81
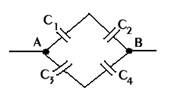
Дана схема соединения конденсаторов (рис 1), в которой С1=5 мкФ, С2=8 мкФ, С3=12 мкФ, С4=10 мкФ. Если С1 и С3 поменять местами, то общая ёмкость:
 1. увеличится на 0,4 мкФ
1. увеличится на 0,4 мкФ
2. уменьшится на 0,4 мкФ=
3. не изменится
4. увеличится на » 0,5 мкФ
5. уменьшится » на 0,5 мкФ
82
Если два конденсатора различной ёмкости соединить параллельно, то их общая ёмкость 16 пФ; а если те же конденсаторы соединить последовательно, то их общая ёмкость 3,75 пФ. Тогда ёмкости конденсаторов различаются:
1. на 2 пФ 3. на 3 пФ
2. на 3,5 пФ 4. на 4 пФ=
83
К конденсатору ёмкостью 2 мкФ приложено напряжение 100 В. Энергия электрического поля конденсатора равна:
1. 10 мДж= 3. 100 мДж 5. 200 мДж
2. 5 мДж 4. 20 мДж
-19-
84
Конденсатор состоит из двух круглых пластин радиусом каждая 2 см, находящихся на расстоянии 4 мм друг от друга. Между пластинами диэлектрик с относительной диэлектрической проницаемостью x=5. Ёмкость конденсатора (пФ) равна:
1. 0,85 3. 14,13=
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.