Расчет оптимальной системы связи. Структура систем связи. Критерии качества приема. Оптимальный приемник Котельникова

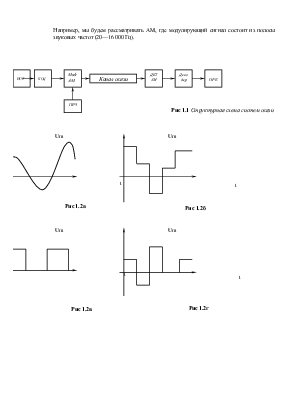
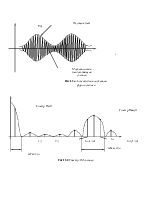
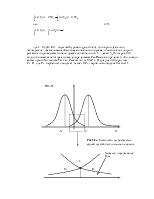
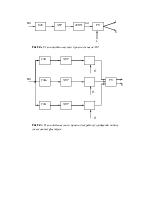
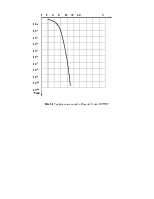
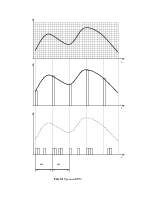
Далее расчитаем по формуле Шеннона,имеющую важное значение в теории информации,так как определяет зависимость пропускной способности от ширины полосы пропускания и мощностных показателей системы(соотношения сигнал/шум).Кроме формула указывает на возможность обмена  полосы на мощность сигнала,однако так как пропускная способность линейно зависит от ширины канала, а от соотношения сигнал/шум – логарифмически.Гораздо эффективен обратный обмен – мощности на полосу пропускания.

Итак , имея формулу Шеннона, рассчитаем пропускную способность для систем с непрерывной передачей сигнала и систем с ИКМ:

Для непрерывного канала:

;

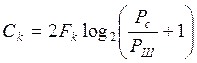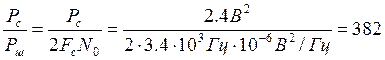
 кбит/с.

Для дискретного канала:

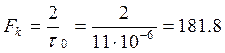 кГц,

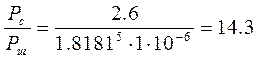
  кбит/с.

Видно что пропускная снособность дискретного канала больше, соответственно он может поддерживать связь на достаточно большой скорости и работать с высокопроизводительными источниками.В этом, собственно и заключается один из смыслов ИКМ.

Теперь перед нами стоит задача в расчете производительности источника , затем согласование с теоремой Шеннона (соответствие  полосы источника полосе канала), проверка избыточности источника,и при случае большой величины последней , устранение ее с помощью статистического кодирование.

Для начала требуется расчитать энтропию источника.

Энтропия источника – это среднее количество информации в сообщении,или мера неопределенности поведения источника. 

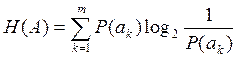 бит/символ

Объем алфавита дискретного двоичного источника  m = 2.

Рассчитаем энтропию :

Теперь необходимо расчитать производительность, чтобы оценить избыточность и необходимость статистического кодирования, а также проверить соответствие каналу.

Производительность источника .Отдельные элементы сообщения на входе источника появляются через некоторые интервалы времени, что позволяет говорить о длительности элементов сообщения. Если средняя длительность одного элемента равна t₀, то производительность источника – это средне количество информации передаваемой в единицу времени:

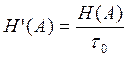  бит/сек расчитаем производительность источника:

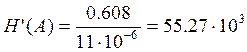   бит/с

Расчитаем избыточность,с ее помощью оценим на сколько эффективно работает источник.

Для начала рассчитаем Н_max(А).Энтропия максимальна в случае, когда появление символов равновероятно. В нашем случае P(1)=P(0)=0.5

Тогда:

0.5 log₂ 0.5+0.5 log₂ 0.5 =1

отсюда избыточность:

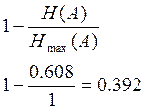
Оценим соответствие скорости в канале производительности источника, с помощью теоремы Шеннона.

Применительно к дискретному источнику она формулируется так: если производительность источника сообщений Н`(С) меньше пропускной способности канала С: 

H`(A)< C,

То существует способ кодирования (преобразования сообщения в сигнал на входе) и декодирования (преобразования сигнала в сообщение на входе канала), при котором вероятность ошибочного декодирования и ненадежность Н(А|Â) могут быть сколь угодно малы. Если же

Н`(А)> С,

То таких способов не существует.

Таким образом, согласно теореме К. Шеннона конечная величина С – это предельное значение скорости безошибочной передачи информации по каналу.

По выше расчитанным данным производительность и скорость в дискретном канале вполне удовлетворяют теореме Шеннона. Производительность невелика и желательно сделать ее больше, приблизив энтропию к максимальной, и более эффективно использовать дискретный канал.

4. Кодирование информации

4.1.Статистическое (эффективное) кодирование

При статистическом кодировании уменьшается избыточность, благодаря чему повышается производительность источника сообщений. При таком методе кодирования пропускная способность канала связи без помех используется наилучшим образом. При оптимальном кодировании (статистическом) H`(A)   – производительность источника  должна быть максимально приближена к пропускной способности канала связи – С (это максимальное количество информации, которое передается по каналу за 1 секунду).

.

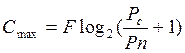Структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.

                                                      4.1.1 Метод Хаффмена

Метод Хаффмена – самый известный метод эффективного (статистического)кодирования, заключающийся в присвоении минимальной длины кодовой комбинации элементам алфавита ,появление которых наиболее вероятно.Код Хаффмена относится к неравномерным кодам.

Рассмотрим алфавит, с присвоенными кодовыми комбинациями составленными в равномерном коде.

Таблица 3  Кодированый алфавит

Составим кодовое дерево.Для начала расположим элементы алфавита в порядке убывания вероятности.Далее по алгоритму складываем вероятности,начиная с наименьших.

a₅=0.6141    0.6141             0.6141             0.6141             0.6141             0.6141             0.6141       1

a₃=0.1083    0.1083             0.1083             0.1083             0.1689             0.2166             0.3855

a₄=0.1083    0.1083             0.1083             0.1083             0.1083             0.1689

a₆=0.1083    0.1083             0.1083             0.1083             0.1083

a₂=0.0191    0.0224            0.0382             0.0606

a₇=0.0191    0.0191            0.0224

a₈=0.0191    0.0191

a₁=0.00337

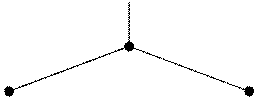
На основе этих расчетов составляется кодовое дерево.Влево отложены ветви с большей вероятностью, вправо, соответственно с меньшей. На конечных узлах образованы элементы с соответствующей вероятностью и длинной кодовой комбинации (Рис.5.1)

Таблица 4 Неравномерно кодированный алфавит

По таблице 4 видно , что условие префексности не нарушено, то есть ни одна кодовая комбинация не является началом другой ,а это одно из условий при построении эффективного кода.

В ходе подобного кодирования получаются неравномерные кодовые комбинации с различными вероятностями.

Определяем среднюю длину кодовой комбинации:

.7мкс

Средняя длина кодовой посылки увеличилась, так как мы учли все кодовые