Основы теории электрических цепей. Переходные процессы. Основные понятия и определения, страница 5

1) единичное, ступенчатое 1(t)

2)+ единичное, импульсное d(t)

3) гармоническое, единичной амплитуды

77.

     Импульсная характеристика цепи h(t) зависит от

1)+ схемы цепи и параметров ее элементов

2) формы напряжений и токов источников, действующих в схеме

3) амплитуды напряжений и токов источников

78.

     Изображение по Лапласу единичной ступенчатой функции 1(t)

1)+

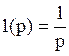
2)

3)

79.

     Изображение по Лапласу единичной импульсной функции d(t)

1)

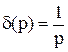
2) +

3)

80.

     Связь между единичной ступенчатой 1(t) и импульсной d(t) функциями

1)+

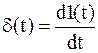
2)

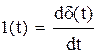
3)

81.

     Если F₁(p) изображение по Лапласу воздействия на цепь в виде напряжения или тока, F₂(p)  изображение реакции цепи (напряжение или ток) при нулевых начальных условиях, то операторная передаточная функция цепи

1)

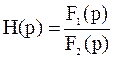
2) +

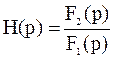
3)

4)

82.

     Если F₁(p)  изображение по Лапласу воздействия на цепь в виде напряжения или тока, и известна передаточная функция цепи H(p), то изображение реакции цепи, напряжения или тока

1) +

2)

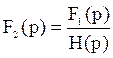
3)

4)

83.

     Если известна передаточная функция цепи H(p), то изображение ее переходной характеристики k(t)

1)+

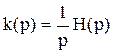
2)

3)

84.

     Если известна передаточная функция цепи H(p), то изображение ее импульсной характеристики h(t) 

1)

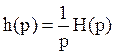
2) +

3)

85.

     Для полного определения цепи достаточно знания ее характеристик

1) переходной k(t) и передаточной функции H(p)

2) импульсной h(t) и передаточной функции H(p)

3) переходной k(t), импульсной h(t) и  передаточной функции H(p)

4)+ любой одной из них

86.

     Если в момент t=0 к цепи c переходной характеристикой k(t) прикладывается постоянное воздействие F в виде напряжения или  тока, то реакция цепи f(t) (напряжение или  ток) определяется по формуле

1)+

2)

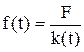
3)

4)

87.

     Если в момент t=t₁ к цепи c переходной характеристикой k(t) прикладывается постоянное воздействие F в виде напряжения или тока, то реакция цепи f(t) (напряжение или  ток) определяется по формуле

1)

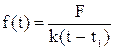
2)+

3)

4)

88.

     Если к цепи прикладывается воздействие произвольной формы f₁(t) в виде напряжения или тока и известна переходная характеристика цепи k(t), то реакция цепи f₂(t)  (напряжение или ток) определяется с помощью интеграла Дюамеля по формуле

1) +

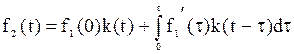
2)

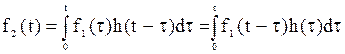
89.

     Если к цепи прикладывается воздействие произвольной формы f₁(t)  в виде напряжения или тока и известна импульсная характеристика цепи h(t), то реакция цепи f₂(t)  (напряжение или ток) определяется с помощью интеграла наложения по формуле

1)

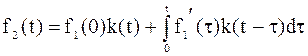
2+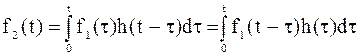

90.

     Спектральный метод анализа переходных процессов предполагает

1) составление  дифференциального уравнения цепи в переходном процессе и решение его известными в математике методами

2) переход от переменных величин к их изображениям по Лапласу, составление операторной схемы замещения цепи и системы алгебраических уравнений относительно изображений переменных

3) получение реакции цепи на воздействие произвольной формы по переходной или импульсной характеристике цепи с использованием интеграла Дюамеля или интеграла наложения

4) +переход от воздействия на цепь как функции времени к ее спектральной плотности по Фурье и получение реакции цепи по комплексной передаточной функции

91.

     Периодическое несинусоидальное колебание можно представить в виде суммы

1) бесконечно большого числа гармонических составляющих

2)+ ограниченного числа гармонических составляющих

92.

     Комплексная амплитуда k-ой гармоники спектра периодического несинусоидального колебания

1) +

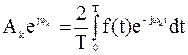
2)

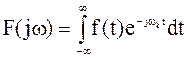
93.

     Амплитудно-частотный спектр несинусоидального колебания это

1) совокупность амплитуд гармонических  составляющих несинусоидального колебания

2) совокупность начальных фаз гармонических  составляющих несинусоидального колебания

3) +совокупность амплитуд и фаз гармонических  составляющих несинусоидального колебания

94.

     Фазо-частотный спектр несинусоидального колебания это

1) совокупность амплитуд гармонических  составляющих несинусоидального колебания

2)+ совокупность начальных фаз гармонических  составляющих несинусоидального колебания