Методы анализа работы узлов аппаратуры связи. Методы анализа работы узлов аппаратуры связи. Определение переходной и импульсной характеристик

График дискретной входной и выходной дискретной функции

2.7 Расчет спектральных характеристик дискретизированного сигнала.

Спектральная плотность дискретного непериодического сигнала U₁(n) может быть найдена по формулам преобразования Фурье следующим образом:

 

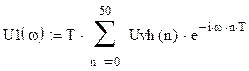(7.1)

Будем изменять частоту в пределах от 0 до 3fв:

Таблица 2.8 – значения спектральных характеристик входного сигнала

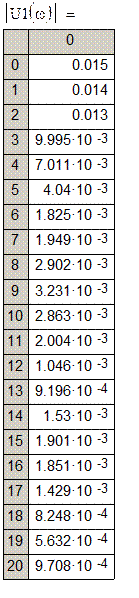
Из данной таблицы (2.8) и таблицы (2.4) видно, что различия в значениях не существенны.

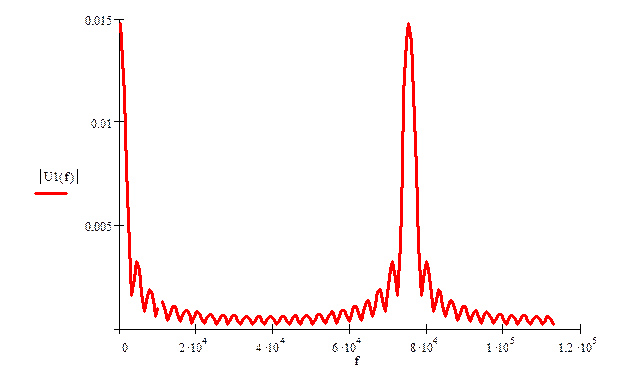
Рисунок 2.17 – График спектральной плотности амплитуд входного дискретизированного сигнала

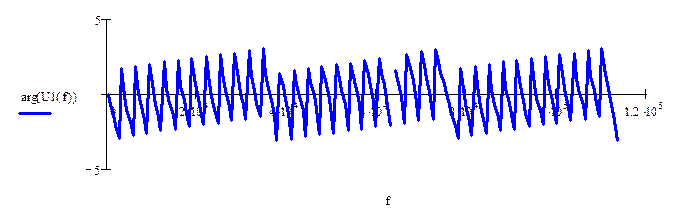
Рисунок 2.18 – График спектральной плотности фаз входного дискретизированного сигнала

2.8 Синтез линейных цифровых фильтров.

В основе простейшего метода синтеза цифровых фильтров лежит предположение о том, что синтезируемый фильтр должен обладать импульсной характеристикой, которая является результатом дискретизации импульсной характеристики соответствующего аналогового фильтра-прототипа:

                                               (8.1)

В общем случае синтез структуры цифрового фильтра осуществляется путём применения Z-преобразования к последовательности вида (8.1)

Находится системная функция цифрового фильтра

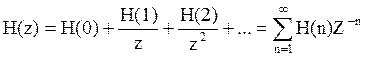                              (8.2)

Найденную системную функцию H(z) следует сравнить с её общим выражением:

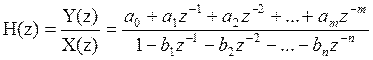                               (8.3)

и определить коэффициенты трансверсальной (a₀, a₁, …, a_m ) и рекурсивной (b₁, b₂, …, b_n)частей H(z)

Степень приближения АЧХ синтезированного цифрового фильтра и характеристика аналогового прототипа зависит от выбранного шага дискретизации Т.

С учетом известных импульсных характеристик h(t), H(n), а также принимая, что n изменяется от 0 до 40 найдем отсчеты функции импульсной хар-ки и выполним Z-преобразования отсчетов

                                                          

{H(n)}=(0.042e-0.125 *0, 0.042e-0.125 *1, 0.042e-0.125 *2, ... , 0.042e-0.125 *40)

H(z)=0.042(1+e-0.125 *1z-1+e-0.125 *2z-2+... +e-0.125 *40z-40)

Получим выражение системной функции

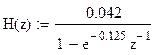                                                     (8.4)

Z - преобразование входного и выходного дискретных сигналов связаны между собой соотношением

                                       

                                                                                                (8.5)

В каноническом виде это выражение имеет вид:

                                                 (8.6)

А значит

Структура формулы (8.6) соответствует алгоритму работы рекурсивного цифрового фильтра, в котором для формирования i-го отсчета используется предыдущее значение не только входного сигнала X, но и выходного сигнала Y.

y_i=a₀x₁+a₁x_i-1+ …+a_mx_i-m+b₁y_i-1+b₂y_i-2+ … +b_ny_i-n

Структурная схема дискретной цепи, реализующая соотношение (8.6) имеет вид (рисунок 2.19)

Недостаток данного принципа реализации является потребность в большом количестве блоков памяти отдельно для рекурсивной и нерекурсивной частей ЦФ. После приведения схемы к каноническому виду схема ЦФ примет вид приведенный на рисунке (2.20).

Коэффициенты масштабных усилителей a_0, a_1, b₁  те же, что и в предыдущей цепи. Блок Т обеспечивает задержку сигнала на интервал дискретизации Т.

Преобразование рекурсивного фильтра к каноническому виду позволяет свести к минимуму требуемое число блоков памяти. Их число будет равно наибольшему из чисел m и n.

X(z)

a₀=0.042 ,  a₁=0 , b₁=0.882

z^-1 – Z-преобразование блока памяти с задержкой на 1 период дискретизации

- сумматор.

Рисунок 2.19 – Z-преобразование дискретной цепи

X(z)

Рисунок 2.20 – Схема дискретной цепи

2.9 Расчет АЧХ дискретной цепи.

Рассчитаем частотную характеристику H(jf) дискретной цепи, имеющей передаточную функцию H(z) вида (8.4). Для этого подставим известные коэффициенты в выражение:

 

Принимая , получим:

(9.7)

Таблица 2.9 – значения АЧХ цифрового фильтра

Рисунок 2.21 – АЧХ цифрового фильтра

2.10 Устойчивость цифровых фильтров.

Дискретная цепь считается неустойчивой, если ограниченное по амплитуде входное воздействие вызывает на её выходе бесконечно нарастающий отклик. И наоборот, цепь устойчива, когда её отклик на ограниченное воздействие также ограничен по амплитуде.

Известно, что у аналоговой устойчивой цепи полюсы передаточной функции располагаются в левой полуплоскости переменной р. При переходе от аналоговой цепи к дискретной и замене преобразования Лапласа Z-преобразованием точки левой полуплоскости р-плоскости переходят в точки, лежащие внутри единичной окружности Z-плоскости. Заметим, что нерекурсивные цифровые фильтры всегда устойчивы, поэтому в проверке на устойчивость нуждаются лишь рекурсивные цепи.

Определим устойчивость цепи, имеющей передаточную функцию вида (8.4):

Полюс передаточной функции найдем, приравняв к нулю знаменатель H(z):

Полюс находится внутри единичной окружности Z-плоскости. Это означает, что цепь устойчива.

Заключение

В ходе данной курсовой работы были систематизированы и закреплены знания, полученные при изучении классического, операторного и спектрального методов расчёта процессов в линейных электрических цепях. Был проведен теоретический анализ дискретных сигналов и линейных дискретных цепей. Я пришла к выводу, что все методы, рассмотренные здесь вполне