Повышение быстродействия в сочетании с технологичностью интегрального изготовления достигается комбинированием двоично-взвешенной матрицы в старших разрядах с матрицей R – 2R в младших разрядах. Такие комбинированные матрицы используются в интегральных ЦАП 594ПА1 (n = 12, tуст = 3,5 мкс) и 1108ПА1 (n = 10, tуст = 0,4 мкс).
8. 4. Применение умножающих ЦАП для
реализации вычислительных операций
В ряде практических применений требуется выполнение вычислительных операций над сигналами, представленными в разной форме – цифровой и аналоговой. Такие операции могут быть реализованы с применением цифро-аналоговых вычислительных преобразователей (ЦАВП). Под цифро-аналоговыми вычислительными преобразователями будем понимать устройства, выполняющие вычислительные преобразования над входными сигналами, представленными в цифровой или комбинированной формах (цифровой и аналоговой), с выдачей результата преобразования в аналоговой форме. Наиболее простую реализацию таких преобразований допускают структуры на базе умножающих ЦАП (УЦАП) и операционных усилителей ОУ. Рассмотрим структурную реализацию типовых математических операций в цифро-аналоговом виде.
Цифро-аналоговое умножение. Эта операция наиболее просто реализуется на базе УЦАП с выходом по напряжению. Входные величины ux и x представлены в различной форме (рис. 8. 7, а), где ux - аналоговая величина, x - n- разрядный двоичный цифровой код.
 а
б
а
б
Рис. 8. 7. Структурная реализация цифро-аналогового умножения
Аналоговая выходная величина УЦАП согласно формулы (8. 2) пропорциональна произведению входных величин
![]() , где
, где
![]() - максимальное значение
десятичного эквивалента цифрового кода.
- максимальное значение
десятичного эквивалента цифрового кода.
Для реализации операции умножения нескольких сомножителей, представленных в цифровом виде, можно использовать схему с каскадным соединением УЦАП, показанную на рис. 8. 7, б. Результаты умножения, формируемые на выходах УЦАП, определяются выражениями:
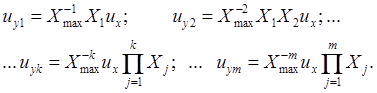
Рассмотрим ряд частных применений схемы, приведенной на рис. 8. 7, б:
а) ![]()
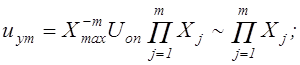
б) X1 = X2 = ...= Xm = X :
![]()
в) ux= Uоп const,X1 = X2 = … =Xm =X :
![]()
Цифро-аналоговое суммирование. Суммирование может быть реализовано по схеме приведенной на рис. 8. 8. Результат суммирования описывается выражением
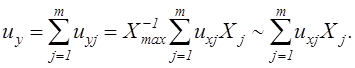
Рассмотрим частные случаи применения сумматора:
а) ux1 = ux2 = ...= uxm = Uоп = const :
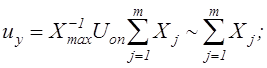
б) ux1 = ux2 = ...=uxm = ux :
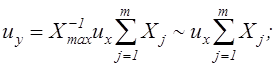
в) X1 = X2 = ...=Xm = X :
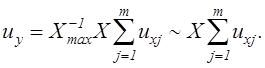
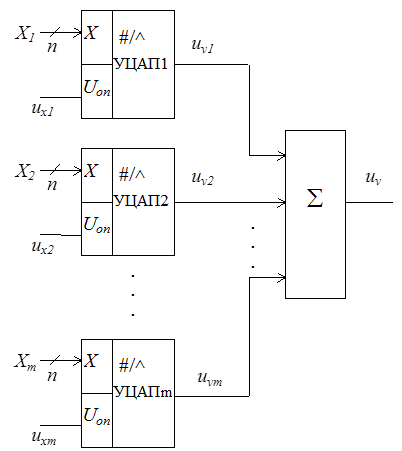 |
Рис. 8. 8. Структурная реализация цифро-аналогового суммирования
Цифро-аналоговое деление. На базе УЦАП цифро-аналоговое деление можно реализовать с использованием принципа обратимости. Для этого УЦАП включается в цепь ООС усилителя (рис. 8. 9, а), и выходное напряжение усилителя подается на вход опорного напряжения УЦАП.
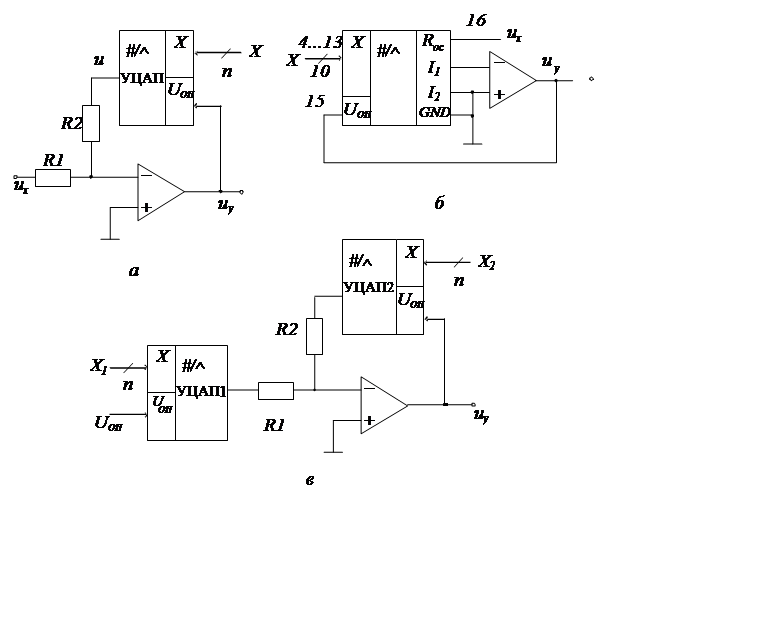
Рис. 8. 9. Устройства цифро-аналогового деления
При этом напряжение на выходе УЦАП равно
![]() или
или ![]()
а ток, протекающий через резисторы R1 и R2, можно определить как
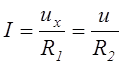 или
или 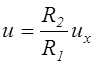 .
.
Следовательно,
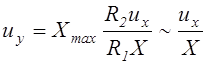 .
.
На рис. 8. 9, б приведен один из вариантов схемы цифро-аналогового деления на базе УЦАП с токовым выходом К572ПА1. В этой схеме ОУ работает в режиме преобразователя выходного тока УЦАП в напряжение, а величина ux подается на вход усилителя через встроенный в УЦАП резистор Rос , играющий роль R1 в предыдущей схеме. Для данного примера реализации
![]()
На рис. 8. 9, в приведена схема деления двух величин, представленных в цифровой форме
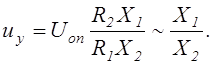
При замене Uоп на аналоговую переменную ux рассматриваемое устройство выполняет множительно-делительное действие над переменными, представленными в разной форме:
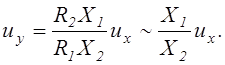
Комбинируя в различных сочетаниях соединение вышерассмотренных операционных схем, можно реализовать и другие типы составных математических операторов.
Контрольные вопросы
1. Назначение, основные параметры и характеристики ЦАП.
2. Схемотехника ЦАП с двоично взвешенной резистивной матрицей.
3. Схемотехника ЦАП с резистивной матрицей R-2R.
4. Сравнительная характеристика ЦАП.
5. В чем состоит отличие обычного ЦАП от умножающего?
6. Примеры реализации вычислительных операций на базе УЦАП.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.