известно,
разность расстояний от фокусов до произвольной точки на поверхности
гиперболоида постоянна, т.е. ![]() , где
, где ![]() – это расстояние между его вершинами.
Расстояние между фокусами гиперболоида
– это расстояние между его вершинами.
Расстояние между фокусами гиперболоида ![]() .
При этом эксцентриситет образующей гиперболы равен
.
При этом эксцентриситет образующей гиперболы равен 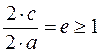 . Наглядно расстояние
. Наглядно расстояние ![]() и
и ![]() представлены
на рисунке 2.2.
представлены
на рисунке 2.2.
Теперь мы можем
отыскать численные значения расстояний ![]() и
и
![]() . Для этого используем
выражение:
. Для этого используем
выражение:
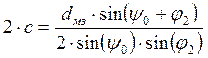 ;
;
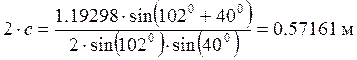
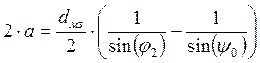 ;
;
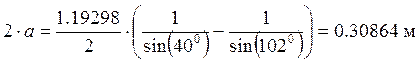
Выполним проверку на условие:
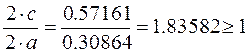 Следовательно, расстояния
найдены, верно.
Следовательно, расстояния
найдены, верно.
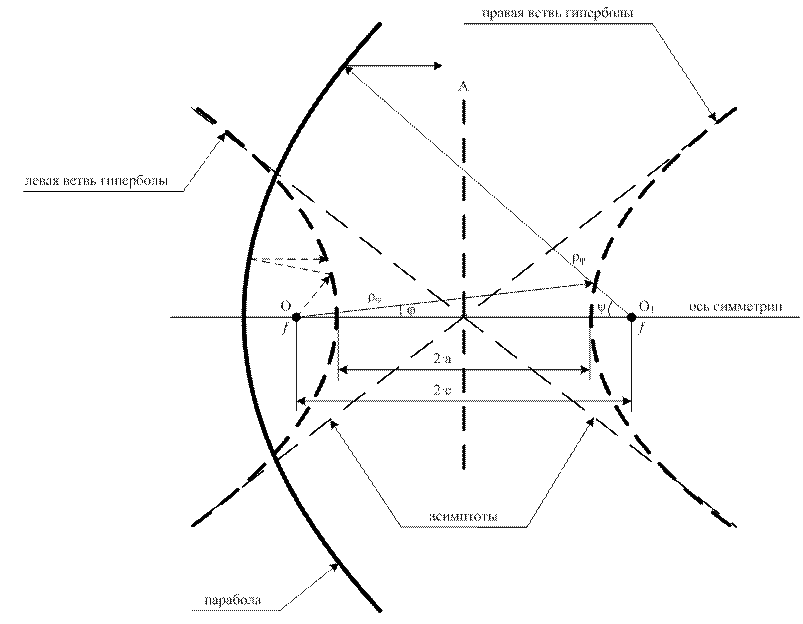
Рисунок 2.2 – Графическое представление расстояний ![]() и
и ![]()
2.4 Расчёт профилей большого и малого зеркал
Данный расчёт производится на основе известных выражений для ρ(ψ) как для большого зеркала, так и для малого зеркала. Эти выражения выглядят следующим образом:
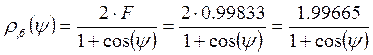 ;
;
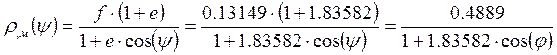 ;
;
для большого и малого зеркал соответственно.
Все расчёты профилей большого и малого зеркал удобно свести в таблицы 2.1 и 2.2
Таблица 2.1 – Результаты расчёта профиля большого зеркала
![]()
Таблица 2.2 – Результаты расчёта профиля малого зеркала
![]()
На основе полученных таблиц можно сделать графики профилей большого и малого зеркал в полярных координатах (рисунок 2.1 и 2.2).
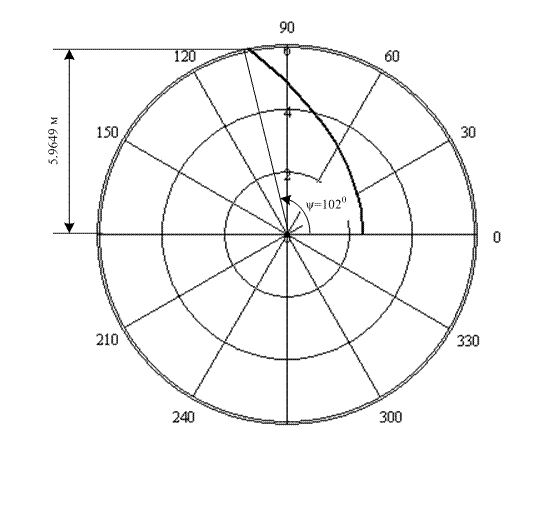
Рисунок 2.1 – Профиль большого зеркала
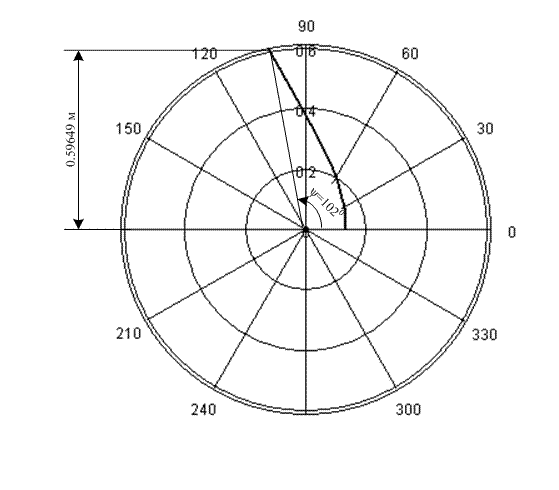
Рисунок 2.2 – Профиль малого зеркала
3 РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ХАРАКТЕРИСТИК, ДОПУСК НА ИЗГОТОВЛЕНИЕ
3.1 Расчёт предельно допустимых значений
Необходимо определить допуск на изготовление:
![]() , где n
определяет технологию производства. Примем
, где n
определяет технологию производства. Примем ![]()
![]()
Найдём максимально возможный КНД по формуле:
![]()
Должно
выполняться условие ![]() , где
, где
![]() , следовательно условие
выполняется.
, следовательно условие
выполняется.
3.2 Расчёт амплитудного распределения в раскрыве антенны
Распределение амплитуд в раскрыве определяется по формуле:
![]() , где
, где ![]()
![]() - относительный радиус,
- относительный радиус, ![]()
Следовательно, амлитудное распределение определится по формуле:
![]()
Изменяя пределы
![]() от 0 до 1, получим зависимость,
которая позволяет нам построить график амплитудного распределения в раскрыве
антенны.
от 0 до 1, получим зависимость,
которая позволяет нам построить график амплитудного распределения в раскрыве
антенны.
Таблица 3.1 – Результаты расчёта амплитудного распределения в раскрыве антенны
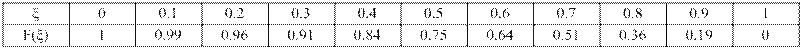
На основе таблицы 3.1 можно построить график амплитудного распределения в раскрыве антенны (рисунок 3.1)
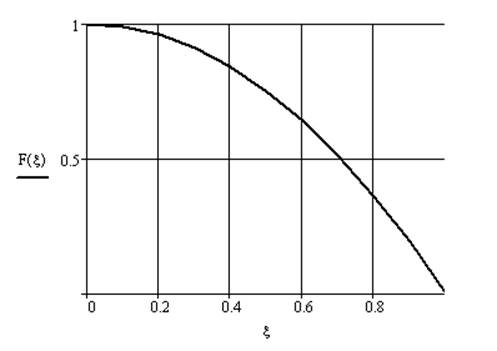
Рисунок 3.1 – Амплитудное распределение в раскрыве антенны
3.3 Расчёт диаграммы направленности антенны
Диаграмма
направленности (ДН) – графическое обозначение ![]() при
при
![]() , где
, где ![]() - есть аналитическое задание
направленности, где
- есть аналитическое задание
направленности, где ![]()
Выражение для расчёта диаграммы направленности антенны будем определять по уровню первых боковых лепестков.
Для УПБЛ= -24,6дБ формула будет иметь вид:
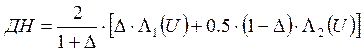 , где
, где ![]()
Следовательно,
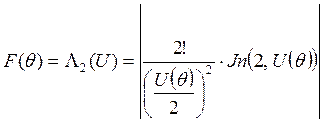 , где
, где
![]() - лямбда-функция II-го порядка
- лямбда-функция II-го порядка
![]() - функция Бесселя второго порядка
- функция Бесселя второго порядка
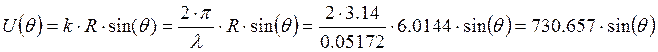
Возьмём изменение
![]() с шагом, равным
с шагом, равным ![]() .
.
По получившимся результатам можно построить диаграмму направленности антенны (рисунок 3.2)
Проверка уровня
первых боковых лепестков: так как ![]() ,
то
,
то
![]() , что
соответствует допустимому уровню первых боковых лепестков (допустимый уровень в
данной курсовой работе составляет -24,6дБ).
, что
соответствует допустимому уровню первых боковых лепестков (допустимый уровень в
данной курсовой работе составляет -24,6дБ).
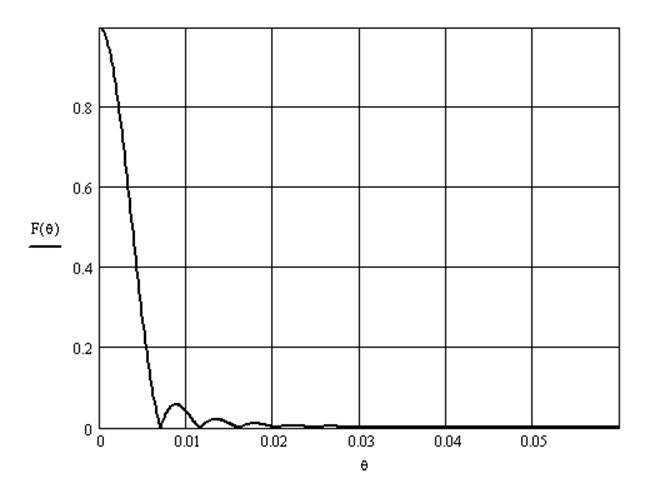
Рисунок 3.2 – Диаграмма направленности антенны
3.4 Выбор типа облучателя и расчет диаграммы направленности облучателя
На первом этапе нужно определить тип облучателя. Из всего многообразия типов и видов облучателей наиболее предпочтительным для моего проекта является конический рупор.
Определим и
графически отобразим главный боковой лепесток оптимального конического
рупора. Определяем на уровне 0.316, так как ДН облучателя должна уложиться в
угол ![]() . Рисунок 3.3 содержит данные для
определения главного лепестка. На нём указаны углы
. Рисунок 3.3 содержит данные для
определения главного лепестка. На нём указаны углы ![]() с
осью рупора
с
осью рупора 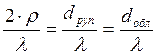 , соответствующего
различным уровням главного лепестка.
, соответствующего
различным уровням главного лепестка.

Рисунок 3.3 - Графические данные для определения главного лепестка
По рисунку 3.3 определяем необходимые данные. Затем рассчитываем диаграмму направленности конического рупора по следующей формуле:
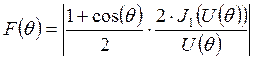 , где
, где
![]() - функция Бесселя первого порядка
- функция Бесселя первого порядка
Затем строим диаграмму направленности конического рупора (рисунок 3.4)
Значение ![]() на уровне
на уровне ![]() равно
равно ![]() .
Исходя из этого, можно определить диаметр конического рупора:
.
Исходя из этого, можно определить диаметр конического рупора:
![]()
Длина облучателя:
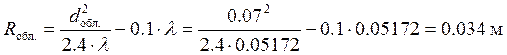
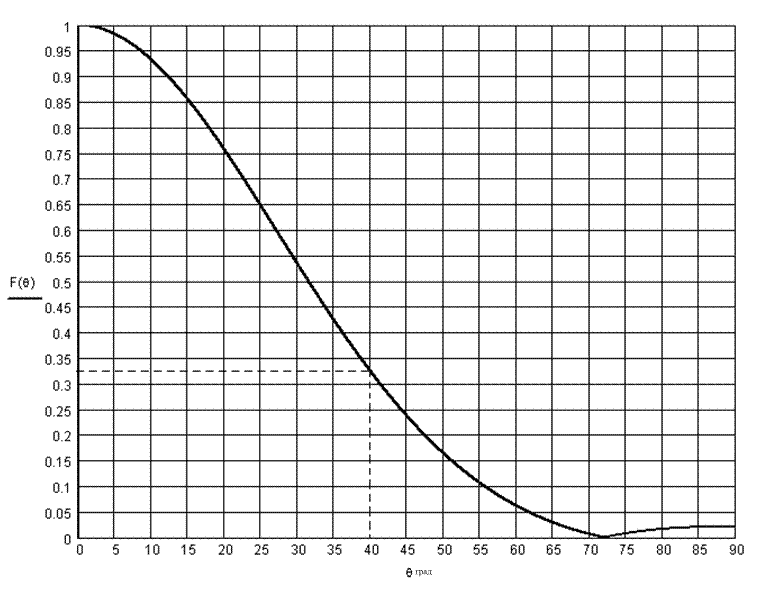
Рисунок 3.4 – Диаграмма направленности конического рупора
3.5 Расчёт антенно-волноводного тракта и его компонент
В качестве волноводных передающих трактов, как правило, используют эллиптические гофрированные волноводы (ЭВГ). Они имеют определённую гибкость, что позволяет придавать волноводному тракту целесообразную конфигурацию, при монтаже требуется минимальное число фланцевых соединений.
Эксцентриситет эллипса:
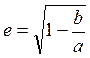 , где
, где
![]() и
и ![]() -
большая и малая полуоси эллипса.
-
большая и малая полуоси эллипса.
Основной волной
является чётная волна сH11.
Для получения достаточно широкой полосы пропускания используют ЭВГ с
отношением полуосей 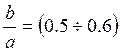 .
При это
.
При это
![]() . Волна сН11 обладает
устойчивостью поляризации, большей допустимой мощностью, чем коаксиальный
кабель, имеет меньшие потери на СВЧ.
. Волна сН11 обладает
устойчивостью поляризации, большей допустимой мощностью, чем коаксиальный
кабель, имеет меньшие потери на СВЧ.
Погонное затухание примерно 4 дб/100м на частоте 6 ГГц. Все эти качества ЭВГ предопределили широкое применение его в качестве волноводных трактов.
Найдём верхнюю и нижнюю частоты:
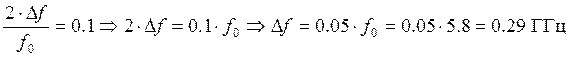
Тогда
![]()
![]()
Критическая частота – максимальная частота, отражённая от слоя при вертикальном падении.
За критическую
частоту возьмём ![]() , тогда
критическая длина волны будет определяться как:
, тогда
критическая длина волны будет определяться как:
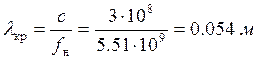
Найдём значение полуосей эллипса:
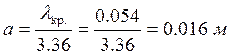
![]()
Волновое сопротивление:
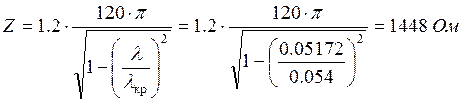
Коэффициент затухания:
ЭВГ изготавливается из меди с удельной проводимостью равной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.