Сверточные коды задаются совокупностью порождающих многочленов gi(X) и характеризуется такими параметрами, как длина кодового ограничения K, скорость R=k0/n0 и свободное расстояние dсв.
Код называется сверточным, так как последовательность кодовых символов {bj} может быть получена как цифровая свертка информационных символов {аj}с импульсным откликом кодера {gij}. Кроме того, значение выходного символа bj с номером t получается как линейная комбинация т предыдущих информационных символов {aj} , i є [t- т,..., t], где т - характеризует память кодера. Длина кодового ограничения Kравна количеству ячеек памяти, содержащихся в кодирующем устройстве.
На рисунке 3.1 приведен пример схемы сверточного кода со скоростью R = 1/2 и длиной кодирующего регистра K=3.
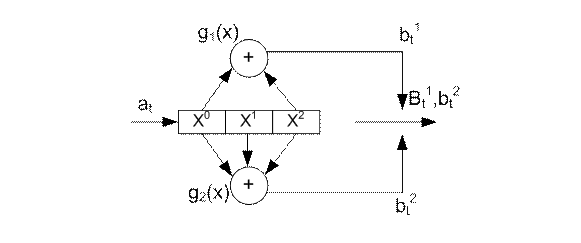
Рисунок 3.1 – Сверточный кодер с R=1/2.
Схема представляет собой регистр памяти для хранения т+1 информационных символов и преобразователь информационной последовательности в кодовую последовательность. Процесс кодирования производится непрерывно. Информационные двоичные символы {ai}поступают на вход регистра сдвига с Kячейками, в котором символы кодовой последовательности формируются суммированием по модулю 2 символов с выходов некоторых ячеек. Подключение сумматоров к ячейкам регистра задается генераторными полиномами g1(x) и g2(x): g1(x)=1+x2 , g2(x)=1+x+x2 или g1(x)=101 и g2(x)=111. За время одного информационного символа на выходе образуются два кодовых символа.
Существуют несколько способов представления сверточных кодов: с использованием кодового дерева (решетчатых диаграмм), с помощью матриц и представление с помощью оператора задержки.
Сверточный кодер можно рассматривать как постоянный во времени конечный автомат, структура которого является периодической и может быть описана с помощью различных диаграмм. Например, сверточный кодер может быть описан диаграммой состояний. Диаграмма представляет собой направленный граф и описывает все состояния кодера, и возможные переходы из одного состояния в другое. Линии переходов (ребра) промаркированы входными символами, которые вызывают данное изменение состояния, и соответствующими выходными символами. Состояние кодера - содержимое К -1 левых (или правых) ячеек регистра памяти. Пример диаграммы состояний показан на рисунке 3.2.
В кружках указаны четыре возможных состояния кодера 00, 10, 01, 11, линиями со стрелками - возможные переходы. Сплошная линия отмечает переходы, совершаемые при поступлении на вход кодирующего устройства информационного символа 0, пунктирная - при поступлении символа 1.
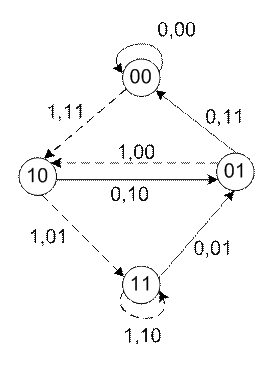
Рисунок 3.2 – Диаграмма состояний сверточного кода.
Решетчатая диаграмма является разверткой диаграммы состояний во времени. На рисунке 3.3 показан пример решетчатой диаграммы.
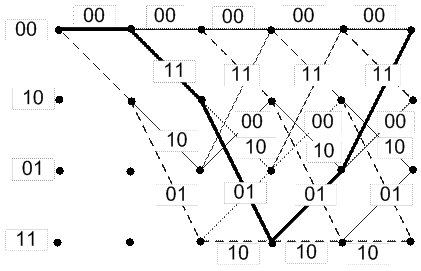
Рисунок 3.3 – Решетчатая диаграмма сверточного кодера с кодовым ограничением 2.
На решетке состояния кодера показаны узлами, а переходы - соединяющими их линиями. После каждого перехода из одного состояния в другое происходит смещение на один шаг вправо. Решетчатая диаграмма дает наглядное представление всех разрешенных путей, по которым может продвигаться кодирование (или декодирование). Каждой информационной последовательности на входе кодера соответствует единственный путь по решетке.
Решетчатая диаграмма удобна для наглядного пояснения принципов декодирования сверточных кодов. Следует отметить, что в двоичном симметричном канале оптимальной оценкой переданной кодовой комбинации слова является комбинация, ближайшая (в смысле расстояния по Хеммингу) к принятой. Это и есть путь по кодовой решетке, отстоящий от последовательности на минимальное расстояние по Хеммингу. Поиск такого максимально правдоподобного пути и составляет сущность алгоритма декодирования Витерби.
4.2. Свободное расстояние сверточного кода.
Мерой помехоустойчивости сверточного кода является, как правило, вероятность ошибочного приема либо отдельного символа, либо блока символов в целом. Однако помехоустойчивость декодирования зависит и от дистанционных свойств кодовых последовательностей на выходе кодера. При этом чаще всего расстояние между последовательностями оценивают с помощью метрики Хэмминга.
Так, свободное расстояние dсв(dfree) - это минимальное расстояние между двумя произвольными полубесконечными последовательностями на выходе кодера, отличающимися в первой ветви. Для коротких кодов свободное расстояние легко определить
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.