Преобразование Лапласа и его основные свойства. Теорема единственности. Дифференцирование и интегрирование оригиналов и изображений

Операционное исчисление является одним из методов прикладного  математического анализа. С его помощью удаётся во многих случаях упростить решение задач, встречающихся в механике, электронике, автоматике и других областях науки и техники. Особое место занимает операционное исчисление при изучении переходных процессов в электротехнике, радиотехнике и импульсной технике.

1 ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА

Определение 1. Функция f(t) называется оригиналом, если она удовлетворяет следующим свойствам:

1.  f(t) определена на (–) и равна нулю на (–);

2.  f(t) либо непрерывна, либо имеет  конечное число точек разрыва первого рода на каждом конечном интервале;

3.  Существуют такие числа  и , что при всех t

Поясним эти условия. Условие 1 вводится в связи с тем, что во многих задачах физики и техники аргумент t рассматривается как время. Поэтому не имеет значения, как ведёт себя функция f(t) до некоторого момента времени, который всегда можно принять равным нулю. Условие 3 накладывает ограничение на характер роста функции f(t) при . Оно означает , f(t) при  растёт не быстрее экспоненциальной функции. Число   называется показателем роста.

Определение 2. Изображением функции-оригинала f(t) называется функция F(p)  комплексного переменного ,  определяемая интегралом

(1.1)

Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа и обозначают  или .

Из определения оригинала следует, что

(1.2)

Пример 1.1. Найти изображение единичной функции Хевисайда:

Решение. Эта функция является оригиналом, так как для неё выполняются все три требования оригинала. Изображение

Пример 1.2. Найти изображение показательной функции

 – комплексное число.

Решение. Имеем, по определению

,

если  или .

Если f(t) – оригинал, то возникает вопрос: для всякого ли оригинала существует изображение. На этот вопрос ответит следующая теорема.

Теорема. Для всякого оригинала f(t) изображение существует в полуплоскости ,  где – показатель роста f(t).

Доказательство. Воспользуемся соотношением 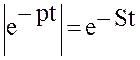 и свойством, что абсолютная величина интеграла не больше интеграла от абсолютной величины. Тогда, при  имеем:

.

Теорема единственности. Если функция F(p) является изображением оригиналов f₁(t) и f₂(t), то эти оригиналы равны во всех точках, где они непрерывны.

Изображения обладают свойствами линейности.

1.  Однородность.

Если , то , где  – любое комплексное число.

2.  Аддитивность.

Если , , то .

Эти свойства вытекают из свойств линейности интеграла.

Пример 1.3. Найти изображение функций , .

Решение. Воспользуемся известными соотношениями

,

.

Найдём изображение , используя формулы примера 1.2 при :

;

.

Тогда

,
.

Аналогично 

.

2 ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ

ОРИГИНАЛОВ И ИЗОБРАЖЕНИЙ

Теорема (дифференцирование оригинала). Если  и  является оригиналом, то

(2.1)

Доказательство. По определению изображения имеем

Применим формулу интегрирования по частям, полагая , , найдём   ,            .

Тогда

.

Используя (1.2) в предыдущем равенстве, получаем

Аналогично можно получить следующие соотношения:

………………………………………………

Пример 2.1. Найти изображение функций , .

Решение. Известно, что , .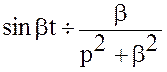

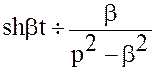Используя правило дифференцирования, получим

.

Аналогично  .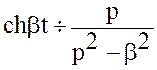

Теорема (интегрирование оригинала).

Если, то

(2.2)

Доказательство. Из свойств интеграла с переменным верхним пределом следует, что 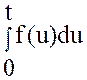– оригинал. Обозначим 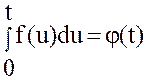. Пусть . Так как , то по предыдущей теореме

Но , отсюда . Или .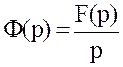

Таким образом .

Формулы (2.1) и (2.2), определяющие изображения производной и интеграла, играют важнейшую роль в операционном исчислении. Из них следует, что взаимно обратным операциям анализа – дифференцированию и интегрированию оригиналов соответствуют взаимно обратные алгебраические операции умножения и деления изображений на p.

Пример 2.2. Найти изображение функции .

Решение. Известно что (пример 1.1)

;

Тогда по (2.2) 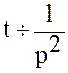 . По аналогии

,    ,   …   ,   .

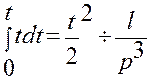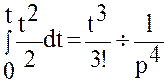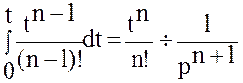Из последнего соотношения вытекает: .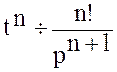

Теорема (дифференцирование изображения).

Если , то .

Доказательство. Найдем изображение произведения :

Следовательно, .

Теорема (интегрирование изображения).

Если  и 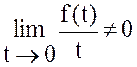, то оригинал .

Доказательство. Пусть .

Обозначим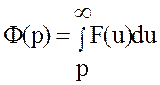

Тогда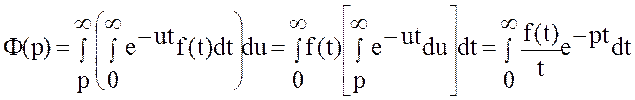

Отсюда  и из определения изображения следует, что

Пример 2.3. Найти изображение функции .

Решение. Используем формулы предыдущих примеров:

;   ;   .

Тогда, используя свойства изображений, получаем:

.

3 ТЕОРЕМЫ ЗАПАЗДЫВАНИЯ, СМЕЩЕНИЯ И ПОДОПИЯ

Рассмотрим оригинал f(t). Тогда функция , определяемая выражением

,

называется оригиналом запаздывающего аргумента. График  получается из графика f(t) сдвигом последнего на величину   вправо вдоль оси t (рисунок 3.1)

 

Теорема запаздывания. Если  – положительное число и , то .

Доказательство. Дано, что . Пусть  – изображение , т.е. 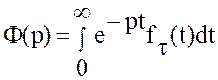. Используя определение , получаем

.

Положим . Тогда .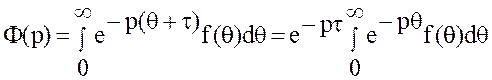

Отсюда и из определения F(p) вытекает утверждение теоремы.

Пример 3.1.  Пусть. Найти изображение оригинала .

Решение. Изображение  есть 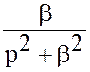. Тогда по предыдущей теореме .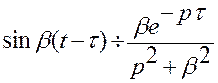

Пусть F(p) изображение некоторого оригинала f(t) и  – любое число. Функция  называется смещением изображения F(p) на число .

Теорема смещения. Пусть . Тогда .

Доказательство. Так как f(t) оригинал, то

Отсюда из свойств 1) и 2) следует, что  – оригинал. Найдём изображение данного оригинала.

По определению имеем

.

Пример 3.2. Дано 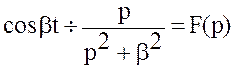. Найти изображение оригинала f(t)=.

Решение. По теореме смещения имеем

.

Теорема подобия. Если , то при любом a>0, .

Доказательство. Пусть, т.е. .

Положим . Тогда   .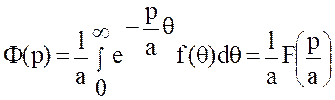

4 ИЗОБРАЖЕНИЕ ПЕРЕОДИЧЕСКОГО ОРИГИНАЛА

Оригинал f(t) называется периодическим с периодом 2L, если для любого t>0 верно равенство .

Пусть требуется найти изображение периодического оригинала. Введём вспомогательную функцию

Тогда , где  – оригинал запаздывания f(t) на число =2L. Тогда благодаря свойству линейности и теореме запаздывания, получаем

.

Отсюда вытекает, что изображение периодического оригинала имеет вид

.

Пример 4.1. Найти изображение оригинала

Решение. Период оригинала  равен . Тогда по формуле изображения периодического оригинала имеем

,	на   [0, ].

Интеграл 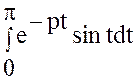     равен , поэтому

.

Таблица оригиналов изображений:

Пример 4.2. Найти оригинал по изображению:

.

Решение. Разложим дробь: 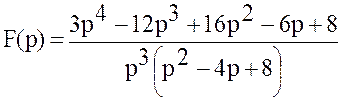 на простейшие:

.

Найдём коэффициенты разложения. Имеем

,
При

Приравнивая коэффициенты при одинаковых степенях p, получим

Решая систему, найдём  , , , , .

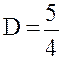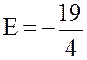Итак, ,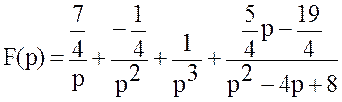

;

;

,

.

Таким образом

.

5 ПРИЛОЖЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

При помощи операционного исчисления можно найти решение задачи Коши линейного дифференциального уравнения с постоянными коэффициентами, т.е. задачи вида

.

(5.1)

Метод решения заключается в следующем: неизвестную функцию