Проектирование НЦФ. Методы расчёта НЦ. Коэффициенты импульсной характеристики фильтра, страница 2

Чтобы избежать его, применим прямоугольную свёртывающую функцию v(k) (рис. 8, е), посредством  которой коэффициенты c_k умножаются на множители функции v(k) при |k| ≤ L и на нуль при |k| > L (рис. 8, з). Этот процесс в свою очередь приводит к сглаживанию передаточной функции H''(w) = H'(w)∗V(w) (рис. 8, ж). Следовательно, множители функции v(k) представляют собой весовую функцию, умножаемую на коэффициенты ряда Фурье. В данном преобразовании эта весовая функция (или "окно") сначала создаёт явление Гиббса, а затем осуществляет сглаживание АЧХ НЦФ. Однако при этом увеличивается ширина переходной полосы и ухудшаются избирательные свойства (степень разграничения полос пропускания и задерживания) фильтра.

Если, например, вместо прямоугольной весовой функции (прямоугольного "окна") использовать треугольное "окно", весовые функции Хемминга, Блэкмана или Кайзера, то это уменьшит колебательный характер у окончательной передаточной функции, но одновременно увеличит в два и более раза ширину промежуточной полосы. Отметим, что прямоугольное "окно" обеспечивает наилучшую среднеквадратическую аппроксимацию требуемой АЧХ при заданной величине N в сравнении с другими "окнами". 

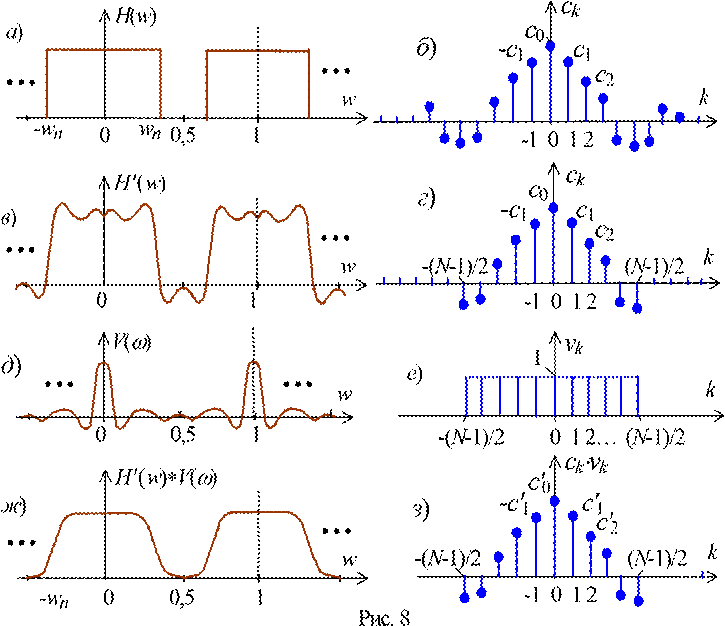
Для физической реализации НЦФ необходимо ограниченную последовательность коэффициентов с_k Фурье (см. рис. 8, г) сдвинуть вправо на L отсчётов. В этом случае комплексная передаточная функция НЦФ может быть рассчитана по формуле

                                                                                  ⎡ L                          ⎤

H'(e j2πw) =⎢ ∑ck cosk2πw⎥e− jL2πw =H'(w)e− jΨ(w) , 0 <w< 0,5.

                                                                                ⎢⎣k=−L                    ^⎥⎦

После умножения коэффициентов с_k ряда Фурье на коэффициенты прямоугольной весовой функции v(k) получим модифицированную передаточную функцию (см. рис. 7, ж)

                                                                                 ⎡ L          sin(πk / L)               ⎤ − jL2πw   − j2πw

                                                 H''(e j2πw) =⎢ ∑ ck                cosk2πw⎥e                       =a0 +a1e                          + ...

                                                                                    ⎢_⎣k=−L πk / L                      ⎥_⎦

+^a_Le− jL2πw +^a_L−1e− j(L+1)2πw + ... +^a_1e− j(2L−1)2πw +^a_0e− j2L2πw =

=H''(w)e ^jΨ(w) , 0 <w< 0,5,                                                               (17) где L = (N - 1)/2; a_k - коэффициенты импульсной характеристики g(k) фильтра, определяемые по формулам: a₀ = с'_L; a_L = с'₀; а_k = с'_{L - k}, k = 1, 2,…, L. 

j2πw

Как отмечалось, передаточная функция H(e ) и АЧХ H(w) НЦФ являются периодическими функциями частоты с периодом, определяемым процессом дискретизации импульсной функции g(k) фильтра с соответствующими ему частотными искажениями. Поэтому на практике передаточная функция имеет смысл только в интервале - 0,5 < w < +0,5, а АЧХ H(w) не имеет смысла за пределами w = 0,5. 

Если выполняется условие a_k =a_N−k−1, то ФЧХ НЦФ

Ψ(w) = - L2πw = - Nπw,(18) т. е. ФЧХ нерекурсивного фильтра с симметричными коэффициентами (можно показать, что и при чётном N, а также при несимметричных коэффициентах а_k =−а_{N −k−1}) является линейной периодической функцией c областью определения для циклической частоты w от -0,5 до 0,5. Поэтому при достижении границ указанного диапазона на графике ФЧХ наблюдается скачок от - π  до + π(см. рис. 6, б).

В соответствии с полученными выражениями(13)…(!8) разработана программа DNF, с помощью которой по заданным требованиям к АЧХ можно определить минимальный порядок НЦФ нижних частот и провести анализ его временных и частотных характеристик. Все вычисления ведутся с числами конечной длины, определяемой разрядностью микропроцессора типа Pentium. Разрядность чисел равна 64 битам (вычисления ведутся с двойной точностью), что позволяет не проводить анализ влияния ограничений разрядности чисел на точность выходных отсчетов. Кроме того, числа с плавающей запятой обеспечивают равномерную относительную точность.