Расчёт однозеркальной параболической антенны. Электрический и конструктивный расчёт пирамидального рупорного излучателя, страница 5

                                                                                                                                                   

                                                                                                               f                                                    

t                                                                                                                         

       

Рисунок 4.2.1. Форма сечения параболического зеркала.

На рисунке 4.2.1 изображён радиус раскрыва зеркала. По ДН облучателя определяется оптимальная угловая апертура ψопт, которая рассчитывается на уровне 10% мощности излучения от максимума (0,316 по напряжённости поля). Такой уровень поля по краю зеркала обеспечивает достаточно низкий уровень боковых лепестков.

Далее рассчитаем фокусное расстояние.

Ψопт = 15° (из ДН)

f =  0,5Ro · ctg0,5 ·ψопт  

f = 0,5 · 14 · ctg(0,5·15) = 53 м , которое нужно откорректировать с тем, чтобы выполнялось равенство:

f = (2n – 1) ·       53 = (2n – 1) ·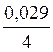  

n = 3,654· , округляем до целого числа 3654  

Теперь уточняем фокусное расстояние:

f = 0,5 · n · λ =  

Форма сечения параболического зеркала:

y =  

y =  

Расчетные данные заносим в таблицу 4.2.1.

Таблица 4.2.1. Расчётные данные формы сечения зеркала.

x	0	0,05	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95
y	0	3,256	6,512	7,975	9,209	10,296	11,278	12,182	13,023	13,813	14,192

 По таблице 4.2.1 строим форму сечения параболического зеркала и изобразим его на рисунке 4.2.2.  Масштабы по осям x и y берём одинаковые.

                               Рисунок 4.2.2. Форма сечения параболического зеркала.

Ниже, в таблице 4.2.2, приведены более подробные данные из расчётов формы сечения зеркала.

Таблица 4.2.2.

Часть отражённых от зеркала лучей, на пути которых  расположен облучатель, перехватывается этим облучателем. Для устранения отражённой от вершины зеркала электромагнитной волны, которая, попадая в тракт питания, ухудшает КБВ, устанавливается компенсирующая пластина диаметром d на расстоянии t.

d =  м

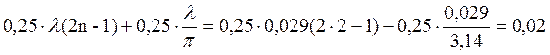t =  м

5. Расчёт диаграммы направленности антенны.                                                           

Поле излучения, создаваемое зеркалом, можно найти, зная наведённый облучателем на его поверхность ток. Вместо тока на «освещённой» стороне зеркала можно рассматривать поле в плоскости раскрыва, которое изменяется электрическими и магнитными эквивалентными поверхностными токами, либо распределением источников типа элемента Гюйгенса. Отсюда два метода расчёта направленности излучателя антенны: токовый и аппертурный (по полю). Однако в обоих методах предполагается, что каждый элемент зеркала действует как элемент плоскости, что даёт лишь приближённый результат. Распределение тока по поверхности зеркала вычисляют по известной характеристике облучателя. На всех этапах расчёта вводится предположение, упрощение и т.п., поэтому расчётные формулы для ДН являются приближёнными. ДН антенны определяется: ДН облучателя, амплитудным и фазовым распределениями в раскрыве антенны, отношением геометрических размеров к длине волны. Для расчёта ДН антенны с пирамидальным рупором типом облучателя применим общий метод расчёта.  Характеристика направленности этой антенны выражается формулой: