
Цель работы: программная реализация метода прогонки и решение тестовых примеров
1. Структура системы линейных уравнений для сеточных значений функции
2. Основное соотношение метода прогонки
3. Вывод расчетных формул прямого хода метода прогонки
4. Вывод расчетных формул обратного хода метода прогонки
5. Заготовка программного блока для метода прогонки
|
№ |
Дифференциальное уравнение |
Граничные условия |
Точное решение |
|
1 |
y''+y= 1 |
y'(0) = 0 y⎛⎜π ⎝ 2 ⎠ ⎝ 2 ⎠ |
1+cosx |
|
2 |
y''+2y'+2y= 2e−x cosx |
y'(0) = 0 y(π)=−e−π |
e−x(cos x+ sin x+xsin x) |
1) С помощью аналитических вычислений проверить точное решение тестовой граничной задачи (определить функцию точного решения и подставить ее в уравнение и граничные условия). Варианты граничной задачи даны в Приложении.
2) Составить программный блок, реализующий метод прогонки для решения граничной задачи ОДУ-2, используя в качестве основы материалы лекции.
3) С помощью программного блока получить численное решение тестовой граничной задачи для числа разбиений N=25.
4) Построить график численного и точного решений.
5) Найти максимальную по сетке абсолютную погрешность численного решения. Если xw, yw – векторы численного решения, а Y(x) – точное решение, то максимальная погрешность вычисляется следующим образом:
⎯⎯→
delta := yw − Y(xw)
⎯⎯→
![]() dmax:= max delta()
dmax:= max delta()
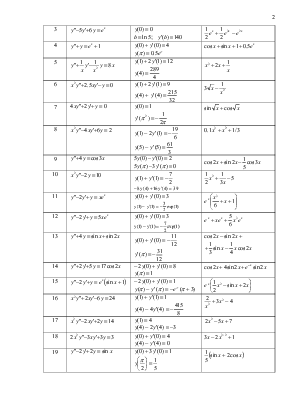
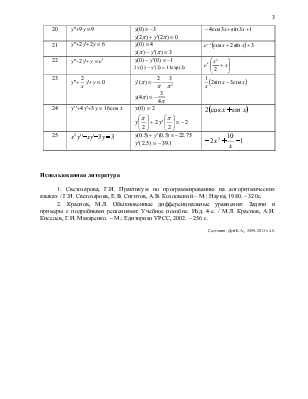
Приложение. Варианты тестовой граничной задачи для ДУ-2
|
3 |
y''−5y'+6y=ex |
y(0) = 0 b= ln5; y'(b) =140 |
|
|
|
4 |
y''+y=ex +1 |
y(0) +y'(0) = 4 y(π) = 0.5eπ |
cos x+ sin x+1+ 0.5ex |
|
|
5 |
|
y(1) + 2y'(1) =12 y(4)
= |
x3 + 2x+ |
|
|
6 |
x2 y''+2.5xy'−y= 0 |
y(1) + 2y'(1) = 9 y(4)
+
y'(4) = |
x |
|
|
7 |
4xy''+2y'+y= 0 |
y(0) =1
|
|
|
|
8 |
x2 y''−4xy'+6y= 2 |
y(1)
−
2y'(1) y(5)
−
y'(5) |
0.1x3 +x2 +1/3 |
|
|
9 |
y''+4y= cos3x |
5y(0) −y'(0) = 2 5y(π)−3y'(π) = 0 |
cos2x+sin 2x− |
cos3x |
|
10 |
x2 y''−2y=10 |
y(1)+ y'(1) =− − 8y(4) +16y'(4) = 39 |
1
2 3x |
|
|
11 |
y''−2y'+y= xex |
y(0)+ y'(0) = 3 y(1) −
y'(1) =− |
ex⎛⎜⎜ |
|
|
12 |
y''−2y'+y= 5xex |
y(0)+ y'(0) = 3 y(1) −y'(1) |
ex +xex + |
|
|
13 |
y''+4y= sin x+sin2x |
y(0)+
y'( y'(π) =− |
cos2x− sin 2x+
|
|
|
14 |
y''+2y'+5y=17cos2x |
−2y(0)+ y'(0) = 8 y(π) = 1 |
cos2x+ 4sin2x+e−x sin2x |
|
|
15 |
y''−2y'+y=ex(sin x+1) |
− 2y(0) +y'(0) =1 y(π) − y'(π) = −eπ(π+ 3) |
ex⎛⎜ ⎝ 2 ⎠ |
|
|
16 |
x2y''+2xy'−6y = 24 |
y(1) +y'(1) = 1 y(4)
−
4y'(4) =− |
2 2
x3 |
|
|
17 |
x2y''−2xy'+2y =14 |
y(1) = 4 y(4) − 2y'(4) =−3 |
2x2 −5x+ 7 |
|
|
18 |
2x2 y''−3xy'+3y = 3 |
y(0) + y'(0) = 4 y(4) −y'(4) = 0 |
3x− 2x3/2 +1 |
|
|
19 |
y''−2y'+2y = sin x |
y(0) + 3y'(0) =1
⎝ 2 ⎠ 5 |
|
|
|
20 |
y''+9y = 9 |
y(0) =−3 y(2π) +y'(2π) = 0 |
− 4cos3x+sin3x+1 |
|
|
21 |
y''+2y'+2y= 6 |
y(0) = 4 y(π) −y'(π) = 3 |
e−x(cos x+ 2sin x)+ 3 |
|
|
22 |
y''−2y'+y =ex |
y(0) −y'(0) =−1 3y(3) −y'(3) =11exp(3) |
ex⎛⎜⎜ |
|
|
23 |
y''+
|
y'(π) =− y(4π) =− |
1
x |
|
|
24 |
y''+4y'+5y=16cos x |
y(0) = 2 y⎛⎜π ⎝ 2 ⎠ ⎝ 2 ⎠ |
2(cos x+sin x) |
|
|
25 |
x2y''−xy'−3y= 3 |
y(0.5) + y'(0.5) =−22.75 y'(2.5) =−39.1 |
−2x3 +10 |
|
Использованная литература
1. Светозарова, Г.И. Практикум по программированию на алгоритмических языках / Г.И. Светозарова, Е.В. Сигитов, А.В. Козловский – М.: Наука, 1980. – 320с.
2. Краснов, М.Л. Обыкновенные дифференциальные уравнения: Задачи и примеры с подробными решениями: Учебное пособие. Изд. 4-е. / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.: Едиториал УРСС, 2002. – 256 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.