Назначение здания и условия эксплуатации. Цех для производства конструкций из клееной древесины

Таким образом, плита удовлетворяет требованиям прочности (первому предельному состоянию).

Определяем прогиб панели от нормативной нагрузки по формуле

Проверяем панель на жесткость по формуле

Таким образом, плита удовлетворяет также и требованиям жесткости (второму предельному состоянию).

4.2.Расчет стропильной балки покрытия.

4.2.1. Статический расчет балки покрытия.

Сбор нагрузок.

			Таблица 4.3
Конструктивные элементы и расчет нагрузок	Нормативная, Н/м2	γf	Расчетная, Н/м2
Постоянная нагрузка
Панель покрытия	941		1093
Клееная дощатая балка покрытия	219	1,1	241
Итого постоянная нагрузка на единицу площади покрытия g	1160		1334
Временная нагрузка
Снеговая нагрузка s	1275	1,6	2040
Полная нагрузка	2435		3374
Полная линейная нагрузка, Н/м	14610		20244

При статическом расчете конструкций постоянные нагрузки определяют по плотности материалов конструкций, а временные – по действующим нормам в строительстве.

Определим собственный вес балки покрытия по следующей формуле:

где  g_с.в. – нормативный собственный вес балки покрытия;

g^н – нормативная постоянная нагрузка;

p^н – нормативная временная нагрузка;

l – пролет;

k_с.в. – коэффициент собственного веса конструкции.

Снеговая нагрузка.

Расчетный район по снеговому покрову – IV.  S₀=1,5 кН/м², а средняя скорость ветра за зимний период v=5 м/с. В соответствии со СНиП [3, пп. 5.1, 5.2, 5.3, 5.5].

, где μ – коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, угол наклона крыши < 25^о , следовательно  μ=1,0;

0,85 – коэффициент СНиП [3, п. 5.5].

 Н/м²

Расчетная распределенная поверхностная нагрузка определяется умножением нормативной нагрузки на соответствующие коэффициенты надежности, принимаемые в соответствии со СНиП [3, пп. 2.2, 5.7].

Коэффициент надежности γ_f для снеговой нагрузки определяется в зависимости от отношения нормативного собственного веса панели g^н к нормативной нагрузке снегового покрова S₀.

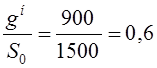 < 0,8  , следовательно, γ_f =1,6.

Рис.4.

Определим расчетный изгибающий момент в середине пролета балки

Определяем поперечную силу на опоре балки

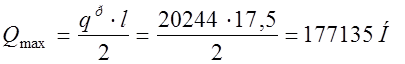, где l=17,5м – с учетом опирания балки.

4.2.2. Конструктивный расчет балки покрытия.

Рис.5.

Высоту балки определяем из условия:

Принимаем h=1,5м.

Ширину балки определяем из условия:

Принимаем b=0,2м

Материал балки покрытия – ель.

Определяем геометрические характеристики.

Момент сопротивления сечения балки:

Момент инерции сечения:     

Момент сопротивления:

               Определим нормальные напряженеия в растянутой зоне по формуле:

где     R_u – расчетное сопротивление древесины изгибу, R_u=1300Н/см²;

m_б – коэффициент условий работы, учитывающий размеры              поперечного сечения(4, п.3.2.д), m_б=0,8;

m_сл - коэффициент условий работы, учитывающий толщину слоев(4,  п.3.2.е), m_сл=1.

          Проверяем скалывающие напряжения по формуле:

где  R_ск=240Н/см² – расчетное сопротивление древесины скалыванию.

Таким образом, балка удовлетворяет требованиям прочности (первому предельному состоянию).

Определяем прогиб балки от нормативной нагрузки по формуле:

тогда относительный прогиб

Таким образом, балка удовлетворяет также и требованиям жесткости (второму предельному состоянию).

4.3. Расчет подстропильной балки.

4.3.1. Статический расчет подстропильной балки.

Сбор нагрузок.

			Таблица 4.4.
Конструктивные элементы и расчет нагрузок	Нормативная, Н/м2	γf	Расчетная, Н/м2
Постоянная нагрузка
Панель покрытия	941		1093
Клееная дощатая балка покрытия	219	1,1	241
Итого постоянная нагрузка	1160		1334
Временная нагрузка
Снеговая нагрузка s	1275	1,6	2040
Полная нагрузка на стропильную балку	2435		3374
Полная сосредоточенная нагрузка на подстропильную балку P, Н	41917		57845
Собственый вес подстропильной балки	167	1,1	183
Линейная нагрузка на подстропильную балку	23		26

Определим расчетный изгибающий момент в середине пролета балки

Рис.6.

Определим поперечную силу

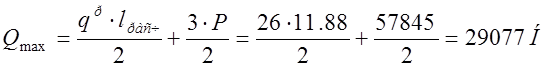        , где l=11,88м – с учетом опирания балки.

4.3.2. Конструктивный расчет подстропильной балки.

Рис.7.

Высоту балки определяем из условия:

Принимаем h=0,8м.

Ширину балки определяем из условия:

Принимаем b=0,14м

Материал балки покрытия – ель.

Определяем геометрические характеристики.

Момент сопротивления сечения балки:

Момент инерции сечения:     

Момент сопротивления:

               Определим нормальные напряженеия в растянутой зоне по формуле:

где     R_u – расчетное сопротивление древесины изгибу, R_u=1300Н/см²;

m_б – коэффициент условий работы, учитывающий размеры              поперечного сечения(4, п.3.2.д), m_б=0,9;

m_сл - коэффициент условий работы, учитывающий толщину слоев(4,  п.3.2.е), m_сл=1.

          Проверяем скалывающие напряжения по формуле:

где  R_ск=240Н/см² – расчетное сопротивление древесины скалыванию.

Таким образом, балка удовлетворяет требованиям прочности (первому предельному состоянию).

Определяем прогиб балки от нормативной нагрузки по формуле:

тогда относительный прогиб

Таким образом, балка удовлетворяет также и требованиям жесткости (второму предельному состоянию).

4.4.Расчет клееной дощатой стойки.

4.4.1.Выбор конструктивной схемы стойки (колонны) каркасного здания.

Стойки деревянных каркасных зданий, как правило, выполняют постоянного