Электроакустические аналогии. Механическая колебательная система. Резонатор Гельмгольца. Акустические аналогии, страница 2

Рассмотрим каждую картинку поподробнее:

а) Резонатор Гельмгольца.

Некая акустическая колебательная система (например, гитара).

l – длина узкой трубки, V – некоторый замкнутый объем, заполненный воздухом, r_M – трение частичек воздуха о трубку. m – масса воздуха в горле резонатора.

В трубку поступает волна, которая выполняет роль пружины, упругого элемента, способствуя концентрации среды в трубке и образуя элементарную массу.

Колебательный процесс в последовательном электрическом контуре

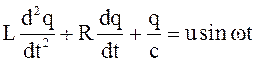.                         (11.3)

Уравнение для  механической колебательной системы, вытекающая из II-го закона Ньютона

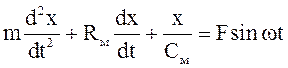.                    (11.4)

Акустические аналогии

Акустическое сопротивление

;  ,                                      (11.5)

электрическое сопротивление

; .                                 (11.6)

Полное сопротивление

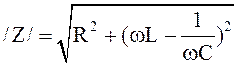,                            (11.7)

его механический аналог

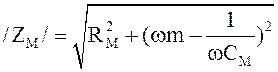,                      (11.8)

Модуль полного сопротивления (11.7) и его механический аналог (11.8) – вытекают из решения уравнений (11.3; 11.4).

Резонансные частоты

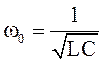,                               (11.9)

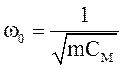,                            (11.10)

где m – масса; С_М – гибкость.

С помощью формальных аналогий (11.3,11.4) и их решений можно проанализировать основные колебательные процессы подвижных узлов микрофонов и громкоговорителей (это два преобразователя, которые мы будем рассматривать), учесть резонансные свойства корпусов. Учитывая (11.9) и (11.10), можно анализировать частотную коррекцию механических и электрических узлов микрофонов и громкоговорителей.

В резонаторе Гельмгольца масса m равна массе воздуха в горле резонатора.

,                                 (11.11)

,                                        (11.12)

где r – вязкость воздуха; r_s – сопротивление излучения; l – длина горла; S – поперечное сечение горла; V – объем полости резонатора.

Гибкость воздуха в полости резонатора. Гибкость, где  – модуль упругости воздуха при адиабатическом процессе (при постоянстве энергии).

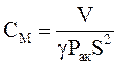,                             (11.13)

собственная частота такого резонатора

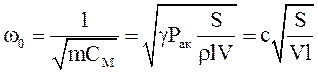,     (11.14)

б) Двойной резонатор Гельмгольца

В отличие от первого, механическую цепочку l₂, S, находящуюся за объемом V, представляют сопротивлением из индуктивности m₂ и сопротивления r_m2, подключенных параллельно емкости С_м.

в) Длинная линия

Волновое сопротивление длинной электрической линии

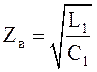,                                (11.15)

где L₁ и C₁ – индуктивность и емкость на единицу длины линии. Заменим их соответственно на их аналоги m₁ и C₁, массу и гибкость на единицу длины трубки. И получим механическое волновое сопротивление:

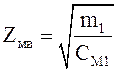,                                      (11.16)

где

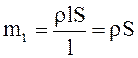,                                   (11.17)

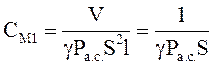,             (11.18)

где V – объем трубы; S – поперечное сечение трубы; l – длина.

Проведем сравнение, т.к , то .

Механическое волновое сопротивление длинной трубы

,                                (11.19)

где S – поперечное сечение звукопровода.

Акустическое сопротивление

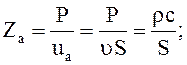                            (11.20)

где  – объемная скорость колебаний.

Z_a в S² раз меньше Z_мв ,т.е если нет отражения от конца трубы (при согласовании нагрузки Z_н=Z_мв), то Z_вх=rсS – входное механическое сопротивление. При наличии отражения от концов трубы, труба будет резонировать на определенных частотах, в зависимости от  ее длины и условий отражения на ее концах, как в случае электрических линий.

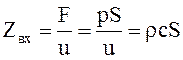.                            (11.21)

г) Акустический фильтр НЧ

д) Акустический полосовой фильтр