Системы связи с использованием шумоподобных сигналов. Сравнительный анализ узкополосных и широкополосных сигналов

Лекция № 16

Тема:   Системы связи с использованием

шумоподобных сигналов

1.  Основные понятия о базе сигнала

2.  Сравнительный анализ узкополосных и широкополосных сигналов

3.  Способы формирования шумоподобных сигналов

4.  Способы приема шумоподобных сигналов

5.  Принципы кодового разделения в системах радиосвязи

1.  Основные понятия о базе сигнала

В системах связи используется такое понятие как база сигнала, которое определяется теоремой Котельникова. То есть исходя из нее любой сигнал с финитным спектром можно разложить на несколько отсчетов, взятых через интервалы времени , где F – верхняя граничная частота спектра сигнала (рис. 1).

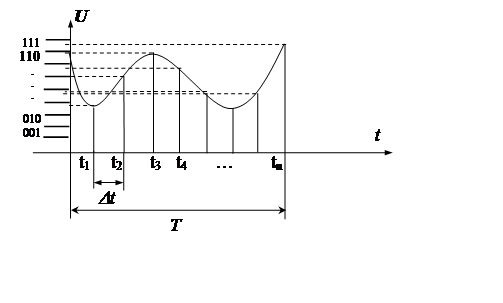Рис. 1. Пояснение к тереме Котельникова

В данном случае, если сигнал существует только в течение времени - Т‚ то количество отсчетов будет равно

                        .                                     (2.1)

Эта величина определяет размерность пространства, в котором представляется сигнал координатами (отсчетами мгновенных значений через временные интервалы ). В этой связи в теории связи эту  величину называют базой сигнала:

                                     .                                      (2.2)

В иных случаях говорят, что величина определяет базис сигнала, т.е. количество осей координат, в котором раскладывается сигнал.

2.  Сравнительный анализ узкополосных и

 широкополосных сигналов

В действующих системах связи, использующих дискретные сигналы значение базы для простых сигналов равно  (рис. 2). Этот же сигнал можно представить в виде сложного сигнала, база которого будет равна -  (см. рис. 2).

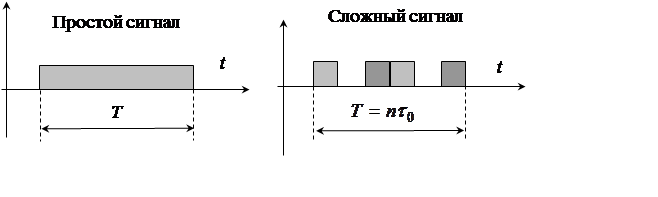Рис. 2. Простой и сложный сигналы

База сигнала указывает на зависимость ширины спектра от длительности сигнала. В случае применения простых сигналов ширина его спектра мала:

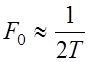                                ,                                           (2.3)

в связи с чем такие сигналы называют узкополосными. Следует заметить, что спектр узкополосного сигнала после модуляции не намного отличается от спектра первичного сигнала.

Для сложных сигналов

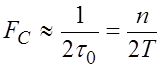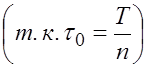                  ,                     (2.4)

В этом случае спектр сложного сигнала как до, так и после модуляции намного превышает спектр первичного сигнала, поэтому его принято называть широкополосным.

3.  Способы формирования широкополосных сигналов

с большой базой

Все сигналы, формируемые на основе ранее применяемых видов модуляции (АМ, ЧМ, ФМ и др.), использующие в качестве переносчика информации гармонические колебания, можно отнести к узкополосным.  В качестве переносчика информации могут служить и другие физические процессы, одним из которых является случайный процесс – шумоподобный сигнал.

Существующие способы формирования шумоподобных сигналов основаны на использовании сигналов с большой базой .

Одним из вариантов формирования шумоподобного сигнала является следующий: информационная посылка первичного сигнала длительностью Tразбивается на n бинарных элементов длительностью 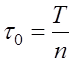 (см. рис. 2).  Такое разбиение позволяет получить сигнал длительностью T с полосой 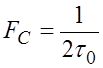 при значении базы . 

Последовательность бинарных элементов образуют коды, выбираемые таким образом, чтобы обеспечить заданные свойства шумоподобного сигнала. Кодовые комбинации сигналов, используемые для передачи сообщения подбирают из условий, чтобы функция автокорреляции каждой из них имела один главный максимум в области , и боковые лепестки с достаточно малыми амплитудами (рис. 3).

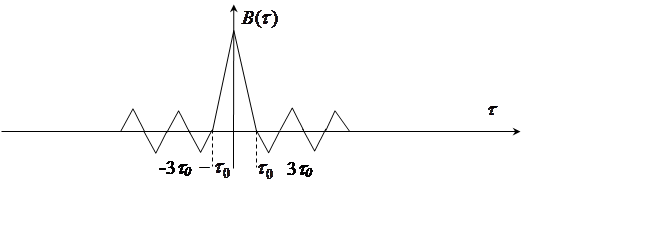Рис. 3. Автокорреляционная функция шумоподобного сигнала

В качестве таких кодов могут служить бинарные последовательности Хаффмена, обладающие следующими характеристиками. Нормированная функция автокорреляции имеет главный лепесток, равный единице, и одинаковые по величине боковые лепестки, равные -  (где N – длина кодовой последовательности).  Значение функции взаимной корреляции между любой парой таких последовательностей равно - (где M – число последовательностей Хаффмена из всей совокупности кодовых комбинаций ). В импульсном режиме работы уровень боковых лепестков не превышает величины .

Кроме сигналов Хаффмена практическое применение находят и другие виды сигналов: последовательности Уолша, Баркера, Лежандра и др.

Шумоподобный сигнала может формироваться на основе известных видов модуляции, с применением так называемой структурной модуляции или модуляции по форме сигнала.

Одним из вариантов такой модуляции может служить следующая пара сигналов:

        ,  ,           (3.1)

где  и  - функции, принимающие значения  в соответствии с заданной кодовой