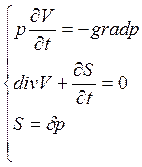Звуковое поле. Количество звуковой энергии в единице объема звукового поля. Акустическое сопротивление, страница 2

                                                (1.12)

Где первое уравнение есть уравнение движения, второе – уравнение неразрывности, третье – уравнение состояния.

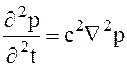                                      (1.13)

Если волна распространяется вдоль оси х:

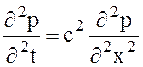                                    (1.14)

Где t – время, x – координата, р – давление.

Общее решение  волнового уравнения для плоской волны:

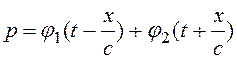                                  (1.15)

Где с – скорость звука (скорость движения волны);

первый член – волна, бегущая в положительном направлении;

второй член – в отрицательном.

Частное решение для волны, распространяющейся в положительном направлении:

              (1.16)

где p_m – амплитуда звукового давления.

,                                           (1.17)

, ,                                        (1.18)

,                         (1.19)

где f – частота;

k – волновое число;

u_m = vU_m – амплитуда скорости колебаний;

U_m – амплитуда смещения.

Удельное акустическое сопротивление, чисто активное:

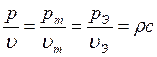,                                (1.20)

для воздуха rс = 413 кг/м²с – волновое сопротивление среды.

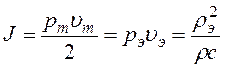,                              (1.21)

где p_э, u_э – эффективные значения;

р и u – действующие значения.

          Сферическая волна.

Фронт сферической волны – сфера, в центре которой находится источник колебаний.

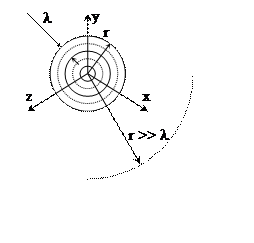l – длина волны

Рис. 3. Распространение сферической волны.

Интенсивность с расстоянием меняется по квадратичному закону:

,                                             (1.22)

где r – расстояние до фронта волны от центра;

J₁ – интенсивность звука на расстоянии единицы длины от центра источника звука.

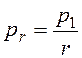, изменяется по гиперболическому закону       (1.23)

Волновое уравнение для трехмерного пространства:

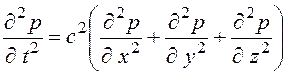,                              (1.24)

при преобразовании координат из прямоугольных в сферические:

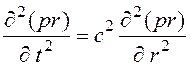,                                    (1.25)

Общий вид решения волнового уравнения для сферической волны:

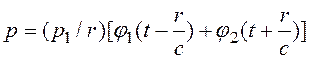,                          (1.26)

где первый член – волна, распространяющаяся от источника;

второй – к источнику звука.

Частное решение, для волны распространяющейся в положительном направлении:

         (1.27)

,                                        (1.28)

где p₁ – амплитуда звукового давления на единичном расстоянии,

r – радиус волны, w – круговая частота.

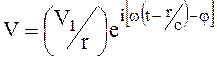,                                (1.29)

,                                        (1.30)

где V₁ – амплитуда скорости колебаний на расстоянии единицы длинны от центра источника звука.

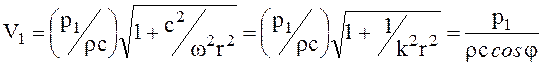    ,         (1.31)

где j – сдвиг фаз между звуковым давлением и скоростью колебаний.

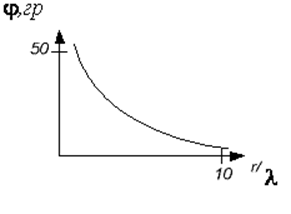
Рис.4. Фазовый сдвиг между давлением и колебательной скоростью в сферической волне.

Чем меньше отношение l/r, тем меньше сдвиг фаз:

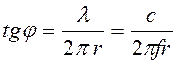,                                      (1.32)

Фронт волны может стать плоским.

Можно рассчитать сдвиг фаз для различных частот.

На средних частотах для расстояний менее 1м сдвиг фаз можно не учитывать.

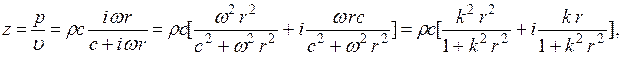             (1.33)

,                                           (1.34)

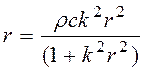,                                            (1.35)

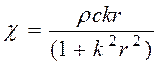,                                         (1.36)

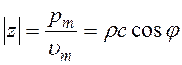,                                      (1.37)

Акустическое сопротивление в сферической волне по величине не превышает акустического сопротивления в плоской волне.

Реактивное сопротивление имеет характер инерционного сопротивления («соколеблющаяся» масса).

Цилиндрическая волна.

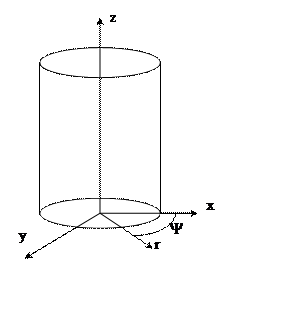
Рис. 5. Распространение цилиндрической волны.

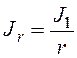,                                             (1.38)

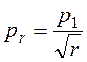.                                           (1.39)

 свидетельствует о том, что мы решаем волноводную задачу.                   

Цилиндрическая волна имеет место при озвучивании пространства с помощью длинных прямолинейных цепочек громкоговорителей.