Анализ сложной электрической цепи. 8 граф схема сложной электрической цепи. Параметры пассивных элементов

2 Анализ сложной электрической цепи.

2.1 Построение схемы

Построим схему для варианта №9, в котором участки цепи предоставлены

Граф расчётной схемы приведён на рис. 8:

Рис. 8 граф схема сложной электрической цепи.

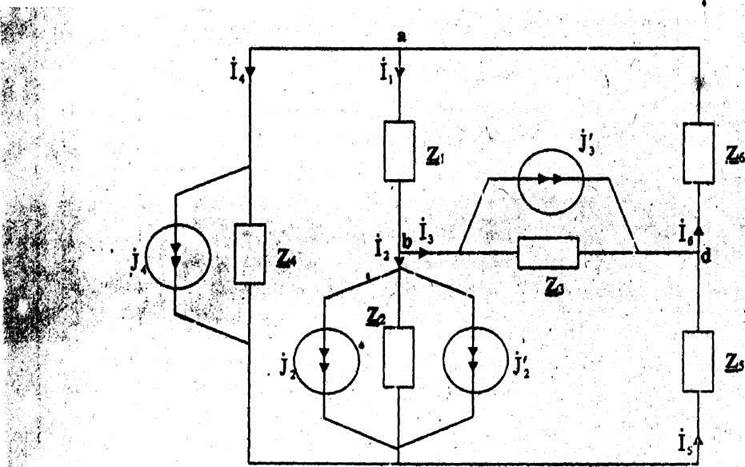
Воспользовавшись видом графа, заменим каждую его ветвь соответствующей заданному коду схемой замещения. Получится схема, показанная на рис. 9:

I."

I,"

I.

Рис. 9 Схема построения сложной электрической цепи.

Параметры пассивных элементов» источников ЭДС и тока:

i .    ; ,•

Определим действующие значения источников ЭДС и тока в схеме:

.71, А.         .       ■

2.2 Анализ схемы методом узловых напряжений. Согласно заданию узел «а» выбираем опорным (базисным). Напряжения между этим узлом и другими узлами (i_h>v_viu_d. За положительное направление этих величин считаем направление к базисному узлу. Преобразованная электрическая цепь для составления системы уравнений по методу узловых напряжений представлена на рис. 10:

Рис, 10 Схема для расчётов по методу узловых напряжений»

Составим систему линейных алгебраических уравнений с комплексными коэффициентами/Число уравнений - 3. Их обищй вид следующий:   ,

Где собственные проводимости узлов i_bb, г^ 'i_mtравны суммам комплексных проводимостей ветвей, присоединённых соотв^твенно к Ь, с» d; общие проводимости узлов х* ^mZ*> 1ы, •&», Г* -£w отрицательны и их значения йо модулю равны сумме проводимостей Bei^V^^^xm*^Y~ п^т,юс соответствующие пары узлов; узловые токи X_k, J_e, V,,, равны алгебраическим суммам источников токов ветвей соединённых со своими узлами, причём знак «плюс» берётся у тока, направленного к узлу, «минус» - у тока, направленного от узла. Следовательно, система йкеет вид:

Подставляем значения комплексных проводимостей и источников тока. Система уравнений принимает следующий вид:

Решая э^ систему находим узловые напряжения: B

По неценным узловым напряжениям вычисляем напряжения в ветвях:

Определим токи ветвей:

2.3 Метод контурных токов.

В соответствии с заданным перечнем ветвей дерева (2, 3, 4) строим граф схемы (рис. 11).                                                                              

Рис. 11 Граф расчётной схемы. а

Рис. 12 Схема для расчётов по методу контурных токов.

Выбор системы независимых контуров (контурных токов) осуществим с  помощью дерева графа. В нашем случае ветви дерева -2,3, 4. Каждому дереву соответствуют связи (хорды) -- ветви графа, дополняющего дерево до полного множества его ветвей (1,5, 6). Основные контуры - это контуры, в которые входит лишь одна хорда, остальные - ветви дерева.

Обозначим токи этих контуров как i_x, i_y, /_z. Условные положительные направления контурных токов выбраны в соответствии направления их связей. Уравнения имс*ит следующий ВИД:              *—---------

Где собственные сопротивления контуров z_xx, z^ , z_n, являются суммой комплексных сопротивлений ветвей, входящих в соответстзующие контуры; общие сопротивления z,, = z,,, z_xt= z«, ^«z^ равны сумме комплексных сопротивлений ветвей, общих для соответствующих контуров, причём берётся знак «минус», если направления соответствующих контурных токов в общих ветвях не совпадают, знак «плюс» - если направления совпадают; контурные ЭДС к_я9 Ь_у> к_г определяются суммами ^ДС всех входящих в контур источников, взятых со знаком «плюс» («MJ снус»), если направление ЭДС совпадает (не совпадает) с направлением ко* турного тока; контурные токи 1_Х, i_y, i_zявляются искомыми величинами. Окончательный вид уравнений для расчётной электрической цепи:

Подставим значения комплексных сопротивлений и ЭДС. Система уравнений примет следующий вид:

ешая эту систему находим контурные токи:

По найденным в результате решения системы контурным токам вычислим ' токи в пассивных элементах ветвей заданной схемы. В ветвях схемы, совпадающих со связями дерева, токи равны контурным токам. В остальных ветвях схемы токи складываются алгебраически из контурных токов, проходящих через ветвь. Знаки слагаемых определяются в зависимости от того, совпадают ли положительные направления контурных токов и токов ветвей (знак «плюс») или не совпадают (знак «минус»).

2.4 Применение теоремы об эквивалентном генераторе для нахождения тока 1$ в ветви ad.

8  соответствии с этой теоремой при определении тока в произвольной ветви аЪ с сопротивлением z_abвсю остальную заданную ЭЦ по отношению к этой ветви можно заменить эквивалентным источником напряжения £_д с

ir

внутренним сопротивлением z.. Таким образом, искомый ток i_ilb-у—*у -

Чтобы найти £,, необходимо разомкнуть ветвь аЪ и вычислить напряжение

0₉  на её зажимах, при этом к.=и.. Сопротивление z, - входное сопротивление по отношению к зажимам пассивного двухполюсника, к которому обращается заданная ЭЦ при условии исключения всех ее¹ источников: источники напряжения закорочены, источники тока разомкнуты.

Чтобы вычислить 0_о, разомкнём ветвь ad.

а

Рис. 13 Схема ЭЦ после обрыва ветви ad.

Для нахождения и. составим и решим по методу узловых напряжений систему, в которой за базисный узел возьмём узел «с», и приравняем у₆ к нулю:

2.5 Проверка баланса активных и реактивных мощностей. В электрической цепи установившегося синусоидального тока каждый её участок - комплексное сопротивление, источник напряжения и источник тока - характеризуются комплексной мощностью, вещественная часть которой равна активной мощности, мнимая - реактивной: s^p+jq. Баланс мощностей устанавливает равенство между генерируемой мощностью источников и потребляемой мощностью пассивных двухполюснике в. Именно: если в цепи п источников напряжений, п источников тока/и/? комплексных сопротивлений, то дслжно выполнятся равенство:

Последнее равенство равносильно двум - балансу активных мощностей и балансу реактивных мощностей:

Для рассматриваемой электрической цепи для пассивных участков имеем:

Вычислим мощность, генерируемую источниками Тока и ЭДС электрической цепи:

Определим относительную погрешность вычисления активной мощности:

Определим относительную погрешность вычисления реактивной мощности:

Следовательно, ошибка при вычислении баланса мощности составляет