


























































Учебно-методическое пособие
Составитель:
Пособие рассмотрено и одобрено методической комиссией факультета информатики.
Декан факультета информатики, доцент
Председатель методической комиссии, профессор
Методическое пособие предназначено в помощь освоению простейших понятий теории вероятностей и ориентировано на студентов факультета информатики. Пособие составлено в форме ответов на варианты контрольных задач, предлагавшихся к решению в течение семестра. Ответы даны в развёрнутом виде с подробными теоретическими и методическими комментариями, что должно помочь при подготовке к экзамену.
Данный документ «выкладывается» в сеть факультета в сессию, начиная с зачётной недели. Студенты, не успевшие к этому моменту решить какие-либо задачи своего варианта, теперь будут решать аналогичные уже на экзамене.
Реализовано пособие в печатном и электронном виде. При работе с электронным вариантом для быстрого листания по разделам документа можно использовать механизм гиперссылок, заложенный в оглавлении. Места ссылок выделены там жёлтой заливкой. Вернуться на начало документа всегда можно с помощью клавиш клавиатуры Ctrl + Home.
©. Ю.В: 2004
Оглавление
вариант № 1.................................................................................. 4
вариант № 2 ................................................................................. 6
вариант № 3 ................................................................................. 7
вариант № 4 ................................................................................. 9
вариант № 5 ............................................................................... 11
вариант № 6 ............................................................................... 15
вариант № 7 ............................................................................... 16
вариант № 8 ............................................................................... 19
вариант № 9 ............................................................................... 21
вариант № 10 ............................................................................. 22
вариант № 11 ............................................................................. 24
вариант № 12 ............................................................................. 27
вариант № 13 ............................................................................. 29
вариант № 14 ............................................................................. 31
вариант № 15 ............................................................................. 32
вариант № 16 ............................................................................. 35
вариант № 17 ............................................................................. 36
вариант № 18 ............................................................................. 38
вариант № 19 ............................................................................. 41
вариант № 20 ............................................................................. 43
вариант № 21 ............................................................................. 44
вариант № 22 ............................................................................. 47
вариант № 23 ............................................................................. 48
вариант № 24 ............................................................................. 50
вариант № 25 ............................................................................. 53
вариант № 26 ............................................................................. 54
вариант № 27 ............................................................................. 57
Литература........................................................................................ 60
вариант № 1
Ответ:
Первый способ решения.
Вычислим искомую вероятность, используя противоположные события. Вероятность
проиграть в 1-м туре есть 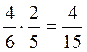 . Иначе вероятность
выйти во 2-й тур есть
. Иначе вероятность
выйти во 2-й тур есть 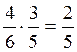 . А вероятность при этом
проиграть во 2-м туре есть
. А вероятность при этом
проиграть во 2-м туре есть 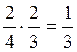 . Тогда вероятность
всё-таки выиграть получается как:
. Тогда вероятность
всё-таки выиграть получается как:
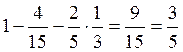 .
.
Второй способ решения.
Вероятность первому вынуть белый шар в 1-ом туре (соб. ![]() )
есть
)
есть 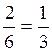 . Вероятность первому вынуть белый шар
при 2-м вытаскивании (соб.
. Вероятность первому вынуть белый шар
при 2-м вытаскивании (соб. ![]() ) есть
) есть 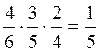 . Вероятность первому вынуть белый шар
в 3-м (последнем) туре (соб.
. Вероятность первому вынуть белый шар
в 3-м (последнем) туре (соб. ![]() ) есть
) есть 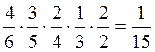 .События
.События ![]() и
и ![]() являются
несовместными, поэтому искомая вероятность может быть вычислена как:
являются
несовместными, поэтому искомая вероятность может быть вычислена как:
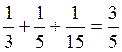 .
.
Ответ:
Событие ![]() , причём у события
, причём у события ![]() элементарных исходов 5; поэтому
искомая вероятность есть:
элементарных исходов 5; поэтому
искомая вероятность есть: 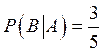 .
.
Ответ:
Прямое преобразование ![]() здесь
есть
здесь
есть ![]() , а обратное ему
, а обратное ему ![]() имеет вид
имеет вид ![]() .
Причём последняя функция имеет положительную производную
.
Причём последняя функция имеет положительную производную 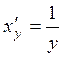 . Тогда по правилу трансформации
плотности НСВ при её монотонно возрастающем преобразовании [1, §12.1] имеем:
. Тогда по правилу трансформации
плотности НСВ при её монотонно возрастающем преобразовании [1, §12.1] имеем:
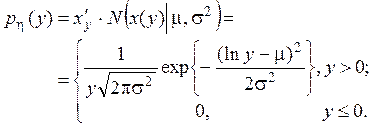 (1.1)
(1.1)
Это и есть плотность логнормального закона распределения; её график и свойства см., к примеру, в [2, с.431; 5].
Логнормальный закон широко используется в теории надёжности; им хорошо аппроксимируется распределение атмосферных помех при распространении радиосигнала. Колмогоров пришёл к этому закону в результате анализа размеров осколков при дроблении породы (то же – и при разрыве снаряда).
Действительно, при элементарном воздействии ![]() на
кусок породы размер осколка
на
кусок породы размер осколка ![]() пропорционален,
очевидно, размеру куска
пропорционален,
очевидно, размеру куска ![]() . Т.е. имеет место
дифуравнение
. Т.е. имеет место
дифуравнение ![]() , решением которого является экспонента
, решением которого является экспонента
![]() . Если воздействие
. Если воздействие ![]() нормально, то это и ведёт к
логнормальному закону для
нормально, то это и ведёт к
логнормальному закону для ![]() .
.
вариант № 2![]()
Ответ:
Прямой подсчёт
по определению Бернулли – Лапласа (с учётом, что достаточно рассмотреть
всего один тур) даёт результат 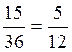 .
.
Ответ:
Обозначим как событие ![]() встречу
в ходе переписи тёмноглазого отца (при этом противоположное событие
встречу
в ходе переписи тёмноглазого отца (при этом противоположное событие ![]() – встреча светлоглазого отца). Далее
обозначим как событие
– встреча светлоглазого отца). Далее
обозначим как событие ![]() встречу в ходе переписи
тёмноглазого
встречу в ходе переписи
тёмноглазого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.