Лабораторная работа №11
«Приближённое решение нелинейных уравнений»
В практической работе радиоинженера зачастую возникает необходимость решения нелинейных уравнений, которые либо трудно, либо невозможно решить аналитически. Решение таких уравнений можно возложить на ЭВМ. Поэтому необходимо иметь представление о методах решения уравнений на ЭВМ.
Любое уравнение можно представить в виде
![]() ,
(1)
,
(1)
где ![]() — некоторая нелинейная
функция. Так
например, для уравнения
— некоторая нелинейная
функция. Так
например, для уравнения ![]() имеем
имеем
![]() . Значение х0
при котором существует равенство f(x0)=0 называется
корнем уравнения. Графически корни уравнения представляют собой абсциссы
точек пересечения графика функции
. Значение х0
при котором существует равенство f(x0)=0 называется
корнем уравнения. Графически корни уравнения представляют собой абсциссы
точек пересечения графика функции ![]() с
осью ОХ (рис. 1), то есть корни уравнения — это нули функции
с
осью ОХ (рис. 1), то есть корни уравнения — это нули функции ![]() .
.
Процесс отыскания корней делиться на два этапа:
1. Отделение корней, т.е. определение отрезка содержащего один корень.
2. Уточнение корня с заданной точностью.
Для первого этапа нет формальных
методов, отрезки определяются или табуляцией, или исходя из физического смысла,
или аналитическими методами. Иногда выявить отрезки, на которых находятся
корни, можно исследованием функции ![]() .
Признаком того, что на отрезке
.
Признаком того, что на отрезке ![]() находится
корень уравнения (1) является неравенство
находится
корень уравнения (1) является неравенство ![]() .
.
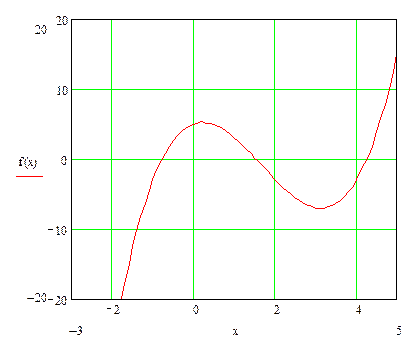 В нашем примере кубического уравнения функция
В нашем примере кубического уравнения функция ![]() представляет собой кубическую
параболу, которая имеет один максимум и один минимум. Для того чтобы найти
положения максимума и минимума приравняем нулю производную функции
представляет собой кубическую
параболу, которая имеет один максимум и один минимум. Для того чтобы найти
положения максимума и минимума приравняем нулю производную функции ![]() :
:
![]() .
.
Решим полученное уравнение: ![]() ;
; ![]() . Поскольку
. Поскольку ![]() ,
, ![]() ,
, ![]() , то на отрезке
, то на отрезке ![]() находится хотя бы
один корень. Из общего вида функции
находится хотя бы
один корень. Из общего вида функции ![]() ясно,
что найденный отрезок содержит только один корень. Для двух других корней
отрезки придётся подобрать. Воспользуемся тем, что при
ясно,
что найденный отрезок содержит только один корень. Для двух других корней
отрезки придётся подобрать. Воспользуемся тем, что при ![]() и
и ![]() функция
функция ![]() возрастает.
Следовательно, если взять достаточно маленький
возрастает.
Следовательно, если взять достаточно маленький ![]() , например,
, например, ![]() , то
, то ![]() и отрезок
и отрезок ![]() содержит корень.
Аналогично подберём довольно большой
содержит корень.
Аналогично подберём довольно большой ![]() ,
так что
,
так что ![]() . Тогда отрезок
. Тогда отрезок ![]() также содержит
корень.
также содержит
корень.
При других функциях ![]() подобное рассуждение,
возможно, провести не удастся. Тогда можно выбрать произвольные достаточно
маленькие
подобное рассуждение,
возможно, провести не удастся. Тогда можно выбрать произвольные достаточно
маленькие ![]() и
и ![]() , и постепенно смещать
их вправо, пока не будет найден нужный отрезок. Критерием пригодности отрезка
, и постепенно смещать
их вправо, пока не будет найден нужный отрезок. Критерием пригодности отрезка ![]() является неравенство
является неравенство ![]() .
.
Второй этап — уточнение корня выполняется различными итерационными методами, суть которых в том, что строится числовая последовательность xi сходящихся к корню x0
Выходом из итерационного процесса является одно из двух условий:
1. │f(xn)│≤ε,
2. │xn-xn-1│≤ε,
Таким образом после
нахождения отрезков локализации корней необходимо сужать эти отрезки до тех
пор, пока либо их длина не станет меньше наперёд заданной величины, которую
будем называть точностью, например ![]() ,
либо значение функции
,
либо значение функции ![]() не
приблизится к нулю с точностью
не
приблизится к нулю с точностью ![]() .
Рассмотрим наиболее употребляемые на практике методы: дихотомии (деления
отрезка пополам), итерации и касательных.
.
Рассмотрим наиболее употребляемые на практике методы: дихотомии (деления
отрезка пополам), итерации и касательных.
Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ε, если известно, что f(a)*f(b)<0
Процесс уменьшения длины отрезка можно произвести следующим образом:
1)
находим середину отрезка ![]() ,
,
2)
находим значения функции ![]() ,
,
3)
если ![]() , то корень находится
в левой воловине отрезка
, то корень находится
в левой воловине отрезка ![]() .
Переносим правую границу отрезка в его середину
.
Переносим правую границу отрезка в его середину ![]() ; иначе переносим
левую границу отрезка в его середину
; иначе переносим
левую границу отрезка в его середину ![]() .
.
4)
Если длина ![]() , то переходим к
пункту 1).
, то переходим к
пункту 1).
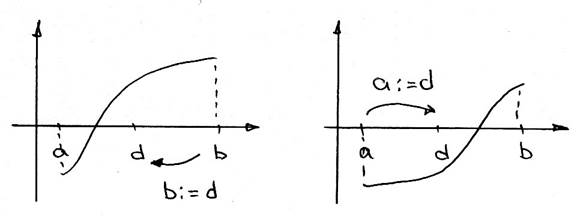
Как только длина отрезка становиться меньше необходимой точности ![]() , можем корнем
уравнения считать любую точку отрезка, например, его середину.
, можем корнем
уравнения считать любую точку отрезка, например, его середину.
Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ε, если известно, что f(a)*f(b)<0
Процесс уменьшения длины отрезка происходит быстрее, если делить его не пополам, а используя хорду. Для этого:
1)
мысленно проводим прямую
между точками ![]() и
и ![]() . Эта прямая
пересекает ось Х в точке
. Эта прямая
пересекает ось Х в точке 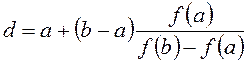 .
Этой точкой отрезок [a,b] разделяется на 2 части,
.
Этой точкой отрезок [a,b] разделяется на 2 части,
2)
находим значения функции ![]() ,
,
3)
если ![]() , то корень находится
в левой части отрезка
, то корень находится
в левой части отрезка ![]() . Переносим
правую границу отрезка в точку d (
. Переносим
правую границу отрезка в точку d (![]() ); иначе переносим
левую границу отрезка в точку d (
); иначе переносим
левую границу отрезка в точку d (![]() ).
).
4)
Если длина ![]() , то переходим к
пункту 1).
, то переходим к
пункту 1).
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a. Определить корень с точностью ε.
x=φ(x) (2).
Выберем грубое, приближенное значение корня x0 , принадлежащее[a,b], подставим его в правую часть уравнения (2), получим:
x1= φ(x0) (3),
далее подставим х1 в правую часть уравнения (3) получим:
x2= φ(x1) (4)
x3= φ(x2) (5)
Проделаем данный процесс n раз получим xn=φ(xn-1)
Если эта последовательность является сходящейся т.е. существует предел
x* =limxn, то данный алгоритм позволяет определить искомый корень.
Выражение (5) запишем как
x*= φ(x*) (6)
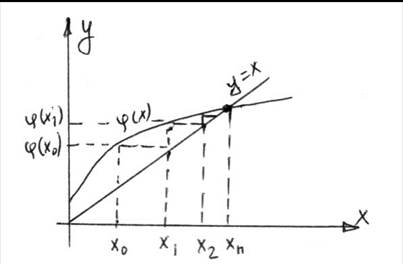
Выражение (6) является решением выражения (2), теперь необходимо рассмотреть в каких случаях последовательность х1…хn является сходящейся. Условием сходимости является выражение если во всех токах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.